初等矩阵的定义

一、文章标题

初等矩阵的定义

二、文章内容

初等矩阵是线性代数中的一个重要概念，在解决线性方程组以及矩阵的运算中都扮演着重要的角色。理解初等矩阵的定义和性质，对于掌握矩阵论的基本知识具有重要意义。

一、初等矩阵的基本概念

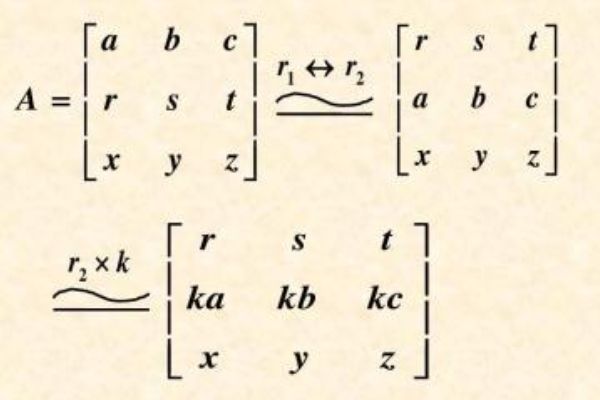
初等矩阵是指通过一次基本的行或列的初等变换所得到的矩阵。初等变换包括行（或列）的倍乘、互换以及行（或列）的加法。具体来说，就是对矩阵进行以下三种操作之一：

1. 倍乘：对某一行（或列）的所有元素乘以一个非零常数。
2. 互换：交换矩阵中两行（或两列）的位置。
3. 加法：将某一行（或列）的若干倍加到另一行（或列）上。

在上述三种操作下，原矩阵就变成了初等矩阵。需要注意的是，初等变换不会改变矩阵的秩和其他基本性质。

二、初等矩阵的性质

初等矩阵具有以下性质：

1. 可逆性：任何初等矩阵都是可逆的，其逆矩阵就是进行相应逆操作的矩阵。这是由于初等变换都是非退化的，不会改变矩阵的秩。
2. 传递性：若将多个初等变换依次进行，所得到的矩阵仍然是初等矩阵。这是因为初等变换是可复合的，复合后的操作仍然属于初等变换的范畴。
3. 重要性：初等矩阵在解线性方程组时具有重要作用。通过将系数矩阵进行一系列的初等行变换，可以将其化为行最简形式，从而方便求解方程组。同时，在计算行列式、计算矩阵的逆等运算中，也会用到初等矩阵的概念和性质。

三、初等矩阵的应用

初等矩阵在数学、物理、工程等领域都有广泛的应用。在数学领域，初等矩阵是线性代数的基本概念之一，是研究矩阵理论、线性方程组的重要工具。在物理和工程领域，初等矩阵被广泛应用于力学、电磁学、信号处理等领域中的矩阵运算和方程求解。

总之，初等矩阵是线性代数中的重要概念，具有可逆性、传递性等基本性质，并且在解决线性方程组、计算行列式、计算矩阵的逆等运算中都有广泛的应用。掌握初等矩阵的定义和性质，对于理解和应用矩阵论的基本知识具有重要意义。