矩阵正交

一、矩阵正交

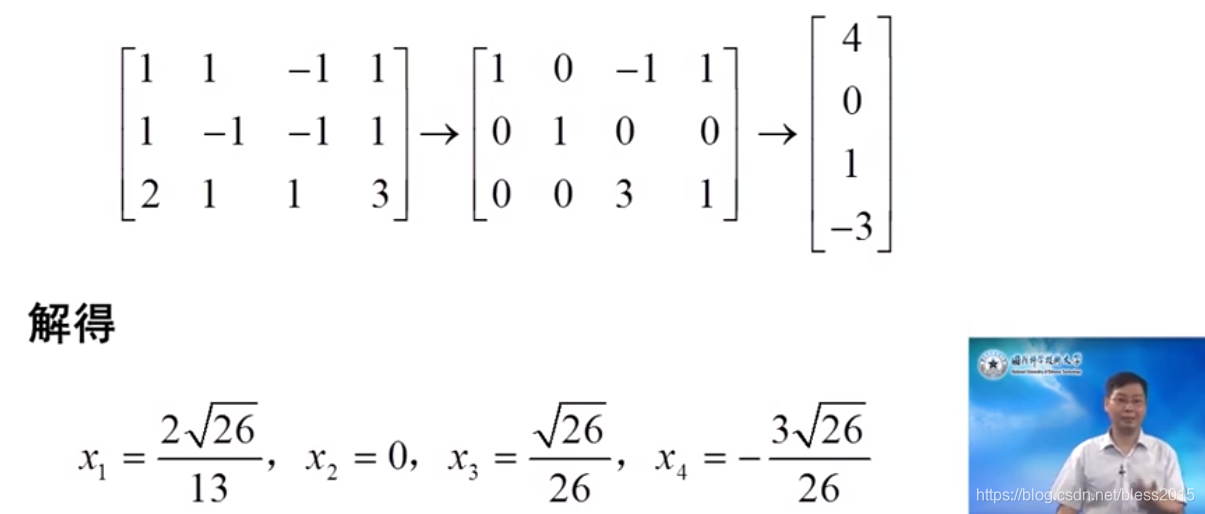
矩阵正交是线性代数中一个重要的概念，涉及到矩阵的乘积和转置等基本操作。本文将介绍矩阵正交的定义、性质以及应用。

一、矩阵正交的定义

在数学中，两个矩阵如果满足一定条件，则称为正交矩阵。具体来说，如果两个矩阵的乘积等于单位矩阵（即它们的行或列向量是线性无关的），则这两个矩阵是正交的。对于实数矩阵，如果其转置矩阵与原矩阵相乘的结果是单位矩阵，则称该矩阵为正交矩阵。

二、矩阵正交的性质

1. 正交矩阵的行列式为±1；
2. 正交矩阵的转置等于其逆矩阵；
3. 正交矩阵的每一列（或行）都是单位向量；
4. 正交矩阵的列（或行）之间相互垂直。

三、矩阵正交的应用

1. 在数值计算中，利用正交变换可以有效地提高算法的精度和稳定性；
2. 在统计学中，主成分分析和因子分析等常用到正交变换；
3. 在信号处理和图像处理中，正交变换也被广泛应用，如离散余弦变换等；
4. 在物理学中，量子力学的波函数常常用正交基来描述。

四、实例分析

以二维向量空间为例，设有两个向量a和b，它们构成一个矩阵A，如果A的转置与A相乘的结果是单位矩阵，则称A为正交矩阵。在实际应用中，我们可以利用正交变换来对向量进行线性变换，使得变换后的向量在新的坐标系下具有更好的性质。例如，在图像处理中，可以利用正交变换对图像进行去噪、增强等操作。

五、总结

本文介绍了矩阵正交的定义、性质和应用。通过正交变换，我们可以有效地提高算法的精度和稳定性，以及在信号处理、图像处理等领域中的应用。正交矩阵的转置等于其逆矩阵这一性质也使得它在很多领域中有着广泛的应用。因此，掌握矩阵正交的概念和性质对于学习和应用线性代数具有重要意义。