残差平方和

文章标题：残差平方和

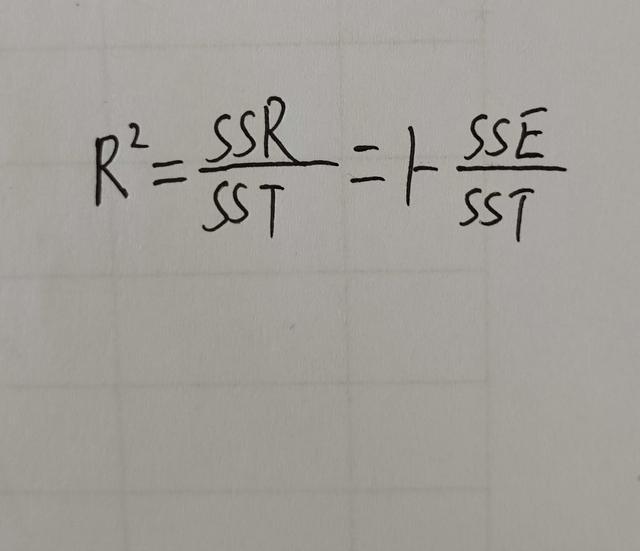
一、什么是残差平方和

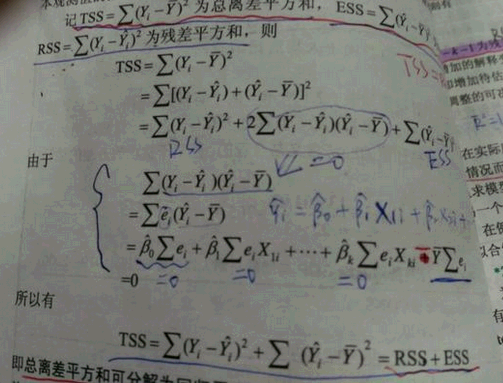
残差平方和（Residual Sum of Squares）是一种用于描述模型预测值与实际观测值之间差异的统计量。在回归分析中，我们通常使用残差平方和来评估模型的拟合程度。简单来说，残差是指模型预测值与实际观测值之间的差异，而残差平方和则是这些差异的平方和。

二、残差平方和的计算方法

残差平方和的计算公式为：SS_res = ∑(y_i - y_hat_i)^2，其中y_i是实际观测值，y_hat_i是模型预测值，∑表示对所有样本进行求和。计算过程中，我们需要先根据自变量和因变量的关系构建一个回归模型，然后使用模型对因变量进行预测，最后计算预测值与实际观测值之间的差异的平方和。

三、残差平方和的意义

残差平方和在回归分析中具有重要的意义。首先，它可以帮助我们评估模型的拟合程度。当残差平方和较小时，说明模型预测值与实际观测值之间的差异较小，模型的拟合程度较好；反之，当残差平方和较大时，说明模型预测值与实际观测值之间的差异较大，模型的拟合程度较差。

其次，残差平方和还可以用于模型选择。在多个模型中选择最优模型时，我们可以比较各个模型的残差平方和，选择残差平方和最小的模型作为最优模型。因为残差平方和最小的模型能够更好地拟合数据，具有更好的预测能力。

四、如何降低残差平方和

降低残差平方和是提高模型拟合程度的关键。我们可以通过以下几种方法来降低残差平方和：

1.增加或减少模型的自变量，选择最优的模型自变量组合； 2.优化模型的参数，使得模型的预测值更接近实际观测值； 3.使用更复杂的模型或非线性模型来提高模型的拟合程度； 4.对数据进行合理的预处理或变换，如去除异常值、缺失值等。

五、总结

总之，残差平方和是回归分析中一个重要的统计量，它可以帮助我们评估模型的拟合程度和选择最优模型。降低残差平方和是提高模型预测能力和应用价值的关键。在具体的应用中，我们需要根据实际情况选择合适的方法来降低残差平方和，从而提高模型的拟合程度和应用效果。