离散值

一、文章标题

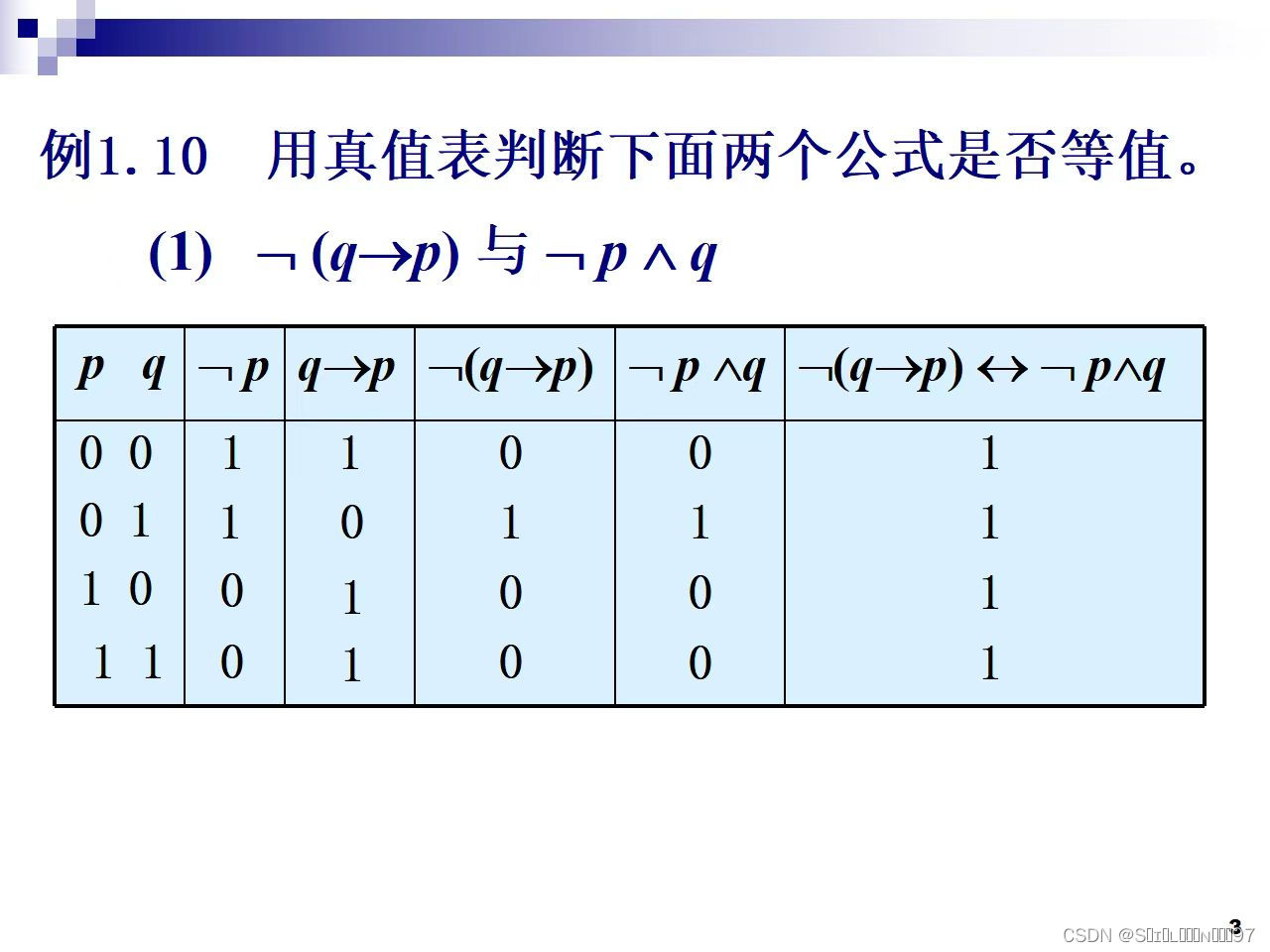
离散值：定义、应用与影响

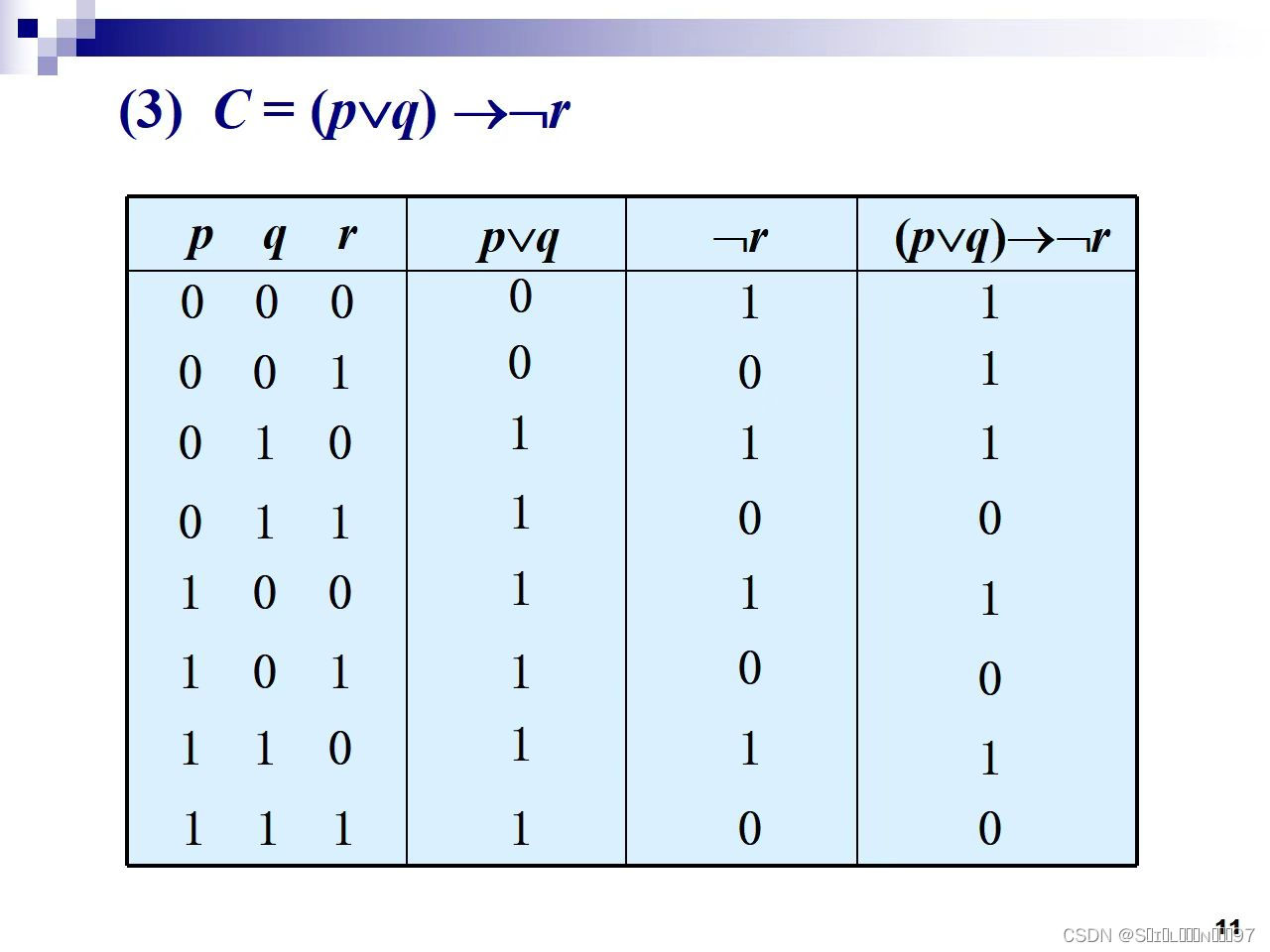
二、文章内容

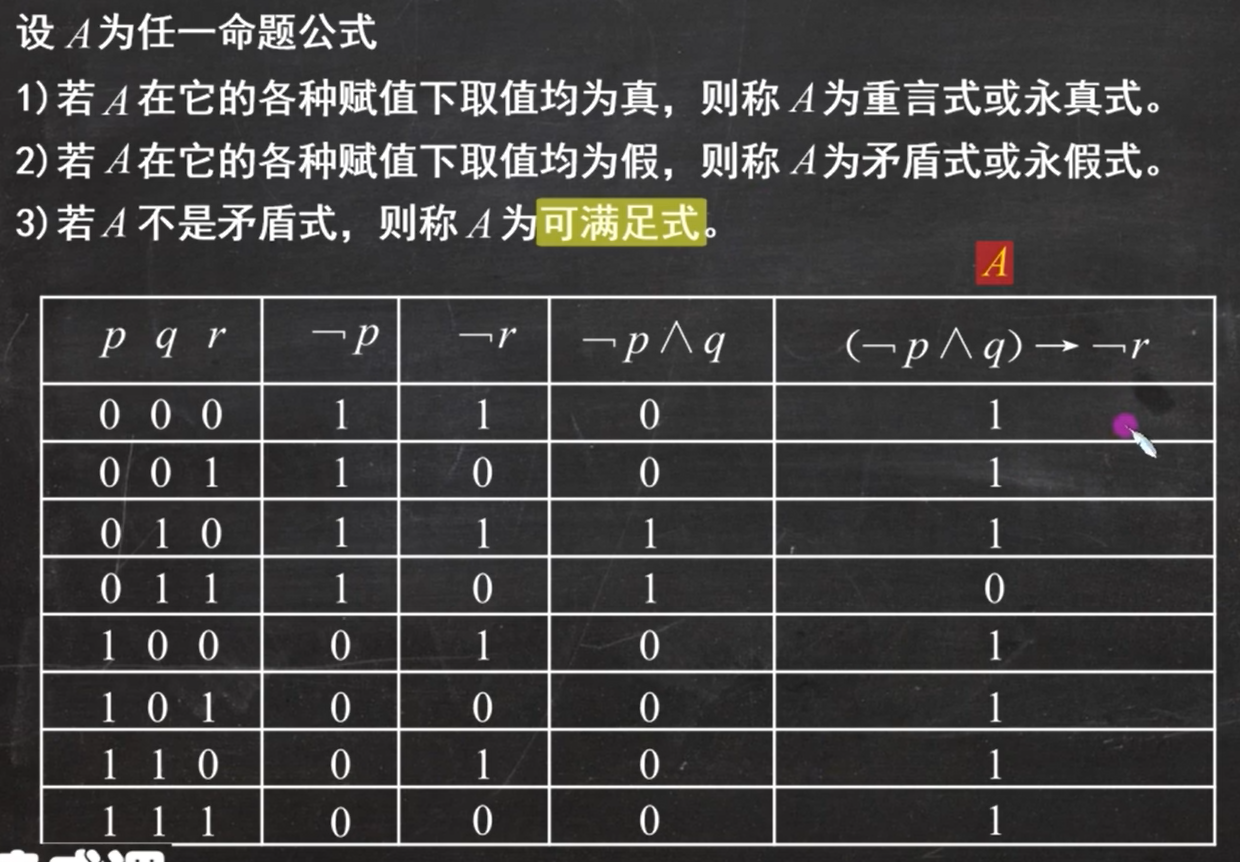
在统计学和数据分析领域，离散值是一个重要的概念。离散值，顾名思义，指的是不连续的数值，与连续值相对。离散值在许多领域都有广泛的应用，如统计学、计算机科学、物理学等。本文将介绍离散值的定义、应用及其影响。

一、离散值的定义

离散值是指一组不连续的数值，这些数值通常以整数的形式出现。与连续值不同，离散值的取值范围是有限的，每个取值之间有明确的间隔。例如，在统计人口数量时，人口数量只能取整数，这些整数就是离散值。

二、离散值的应用

1. 统计学：在统计学中，离散值被广泛应用于概率计算、数据分类、抽样调查等方面。通过对离散值的分析，可以得出各种统计规律和结论。
2. 计算机科学：在计算机科学中，离散值被用于表示计算机程序中的各种状态和事件。例如，在编程中，我们经常使用离散值来表示不同的颜色、按钮状态等。
3. 物理学：在物理学中，离散值被用于描述物理现象的离散性质。例如，在量子力学中，粒子的能量和动量通常是离散的，这些离散值对于理解量子现象具有重要意义。

三、离散值的影响

离散值在各个领域都有着广泛的应用和影响。首先，在数据分析中，离散值可以帮助我们更好地理解数据的分布和规律，从而得出更准确的结论。其次，在计算机科学中，离散值是计算机程序的基础，对于计算机程序的设计和实现具有重要意义。此外，在物理学中，离散值的观念对于理解微观世界的量子现象至关重要。

总之，离散值是一个重要的概念，它在各个领域都有着广泛的应用和影响。通过深入了解离散值的定义、应用及其影响，我们可以更好地理解数据的本质和规律，为各个领域的发展提供有力的支持。