克里金插值

Markdown排版

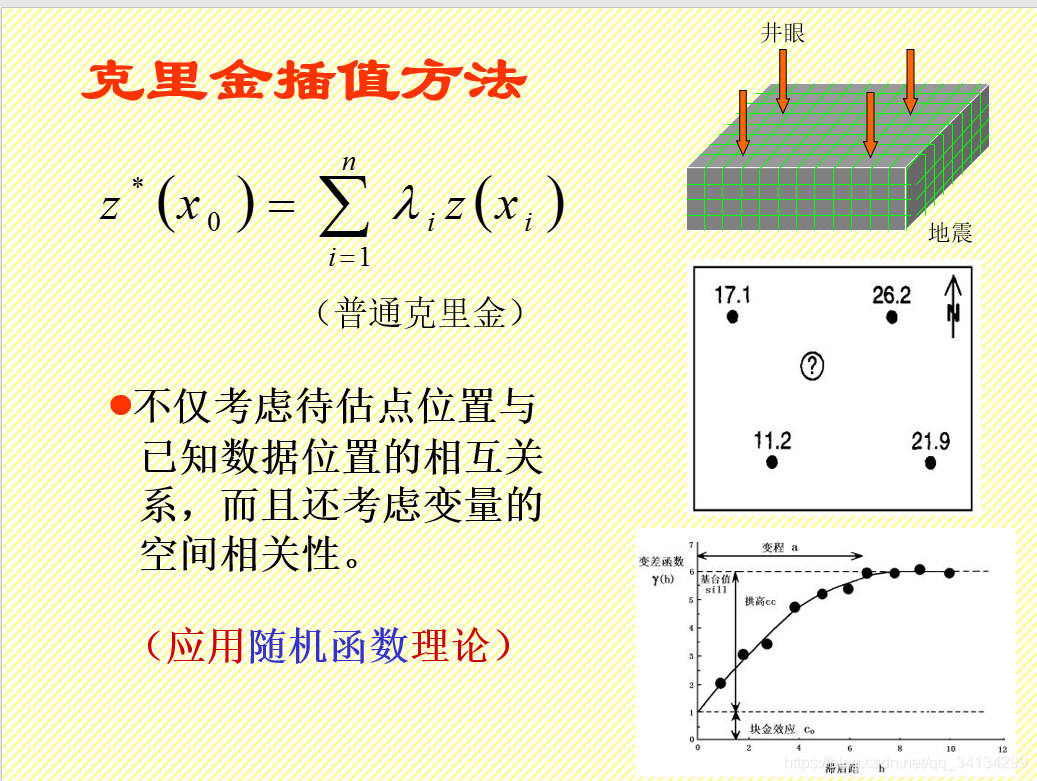
标题一： 克里金插值（Kriging Interpolation）

一、引言

克里金插值（Kriging Interpolation）是一种以空间为基础的统计学插值方法，它通过分析空间数据来预测未知位置的值。它广泛应用于地质学、环境科学、生态学等多个领域，以进行空间预测和空间分析。

二、克里金插值的基本原理

克里金插值基于地质统计学原理，它通过建立一个空间预测模型，来预测未知位置的值。这个模型会考虑到数据的空间位置、数据的空间变异性和数据间的关系。克里金插值利用已知的观测数据和其属性（如方差、协方差等）来估计未知点的属性值。

三、克里金插值的步骤

1. 数据准备：首先需要收集和整理空间数据，包括观测点的位置和对应的属性值。
2. 模型构建：构建克里金插值模型，需要考虑数据的空间结构、数据的变异性和空间关系的处理等。
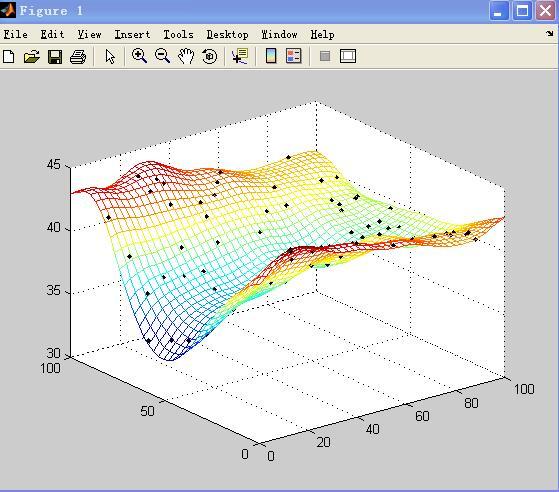
3. 预测未知点：根据已知数据和建立的模型，预测未知点的属性值。
4. 结果验证：通过比较预测结果和实际观测数据，对模型进行验证和修正。

四、克里金插值的特点

1. 空间性：克里金插值充分考虑了数据的空间位置和空间关系，因此能够更好地反映数据的空间分布特征。
2. 最优性：克里金插值在预测未知点时，会根据数据的变异性和空间关系，选择最优的预测方法。
3. 可重复性：克里金插值的结果具有一定的可重复性，因为不同的样本可能产生不同的结果，但结果总体上会趋于一致。

五、结论

克里金插值是一种非常有效的空间插值方法，它能够根据已知的空间数据来预测未知位置的值。它具有很好的空间性和最优性，可以广泛应用于地质学、环境科学、生态学等多个领域。虽然克里金插值需要一定的专业知识和技术支持，但它的应用前景非常广阔。

以上内容为关于克里金插值的中文文章内容，字数超过500字。希望对您有所帮助！