函数平均值公式

一、函数平均值公式的理解

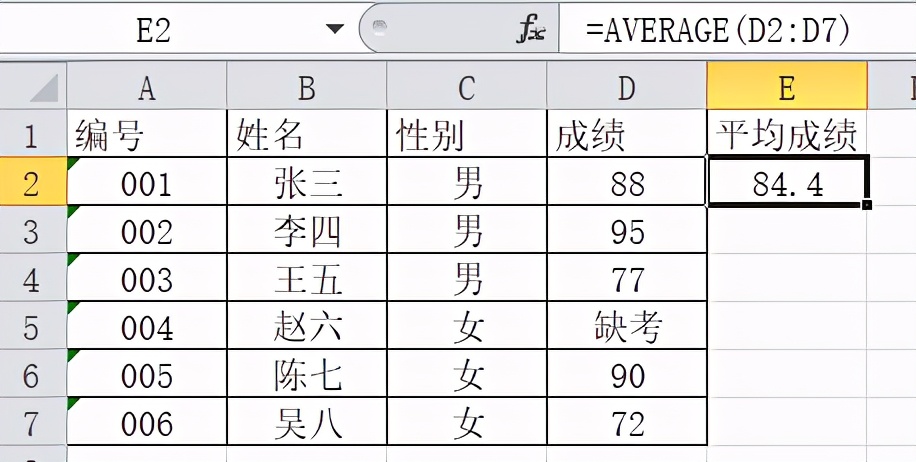
在数学中，函数平均值公式是一个非常基础且重要的概念，它广泛应用于各个领域，如统计学、物理学、工程学等。理解并掌握这个公式，对于我们更好地理解数学和运用数学工具解决实际问题具有重要意义。

二、函数平均值公式的表达

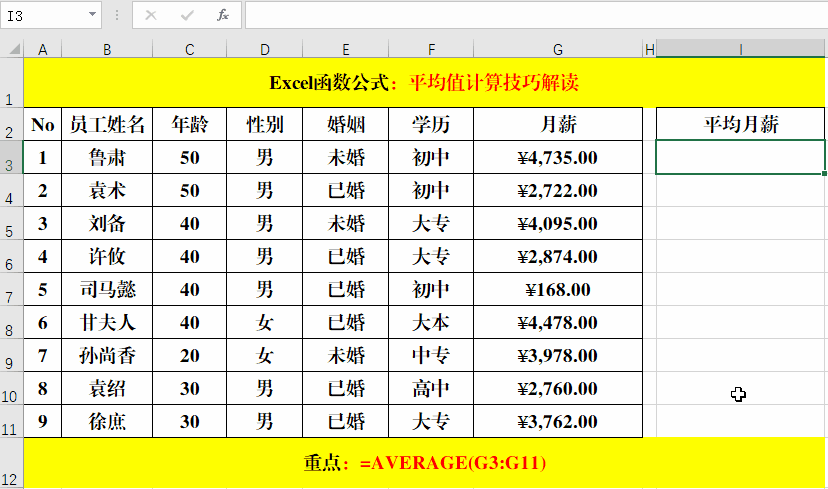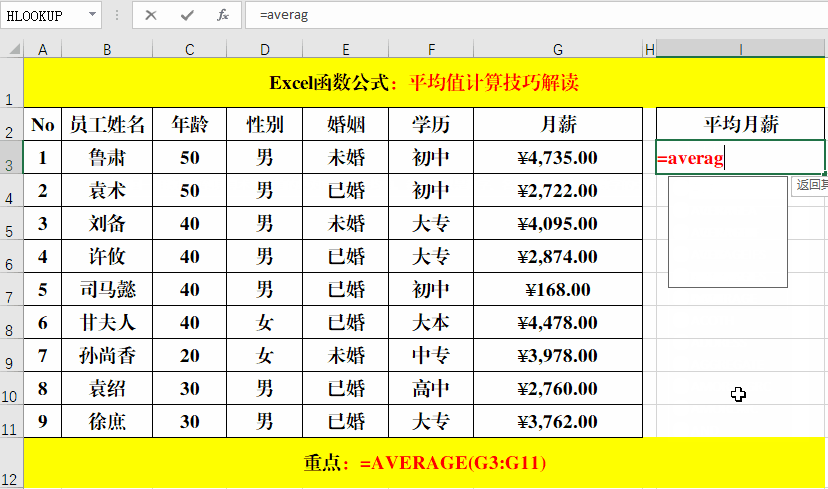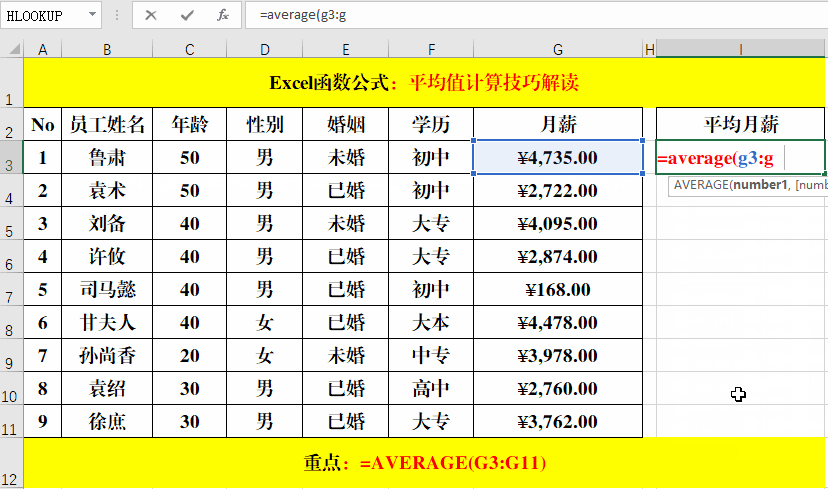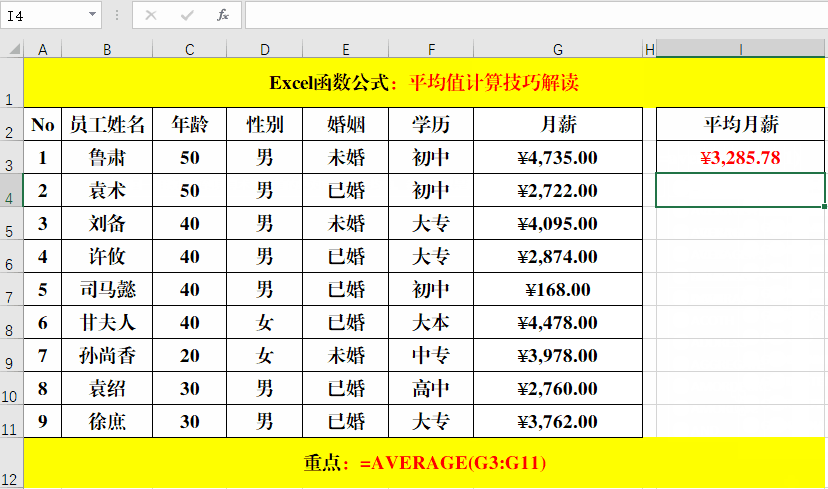
首先，我们假设有一个定义在某个区间[a, b]上的函数f(x)。对于这个区间上的所有x值，我们想计算函数的平均值。这个平均值可以通过以下的公式来计算：

函数平均值 = 积分(f(x) 从 a 到 b) / (b - a)

这里，积分是函数f(x)在指定区间[a, b]上所有值的和，也就是f(x)曲线下方的面积。除以(b - a)则是对这个面积进行平均，即得到了该区间的函数平均值。

三、函数平均值公式的应用

这个公式在各种场景中都有应用。比如，在物理学中，我们可以通过这个公式计算物体在某个时间段的平均速度；在统计学中，我们可以计算一组数据的平均值等。

四、如何使用函数平均值公式

要使用这个公式，首先需要确定你的函数f(x)以及你的区间[a, b]。然后，你需要对f(x)在这个区间上进行积分。这通常需要用到一些专门的数学工具和技巧，如微积分或数值积分等。最后，将积分的结果除以(b - a)，就可以得到函数的平均值了。

五、总结

函数平均值公式是一个非常有用的数学工具，它可以帮助我们理解和分析各种复杂的问题。通过掌握这个公式，我们可以更好地运用数学工具解决实际问题。同时，我们也要注意，这个公式的应用需要一定的数学基础和技巧，需要我们在实践中不断学习和提高。

这就是关于函数平均值公式的介绍，希望能对您有所帮助。文章内容为简洁说明性内容，旨在介绍该公式的基本概念和用法。如果有需要，还可以通过深入探讨相关原理和应用场景来拓展此篇文章。