伪逆矩阵

伪逆矩阵

一、什么是伪逆矩阵

在数学领域，伪逆矩阵（或称为广义逆矩阵）是一种在非满秩矩阵中，用来描述线性方程组解的数学工具。当我们的矩阵不是方阵或者不是满秩的，我们无法直接求出其逆矩阵，但我们可以求出其伪逆矩阵来近似地解决问题。

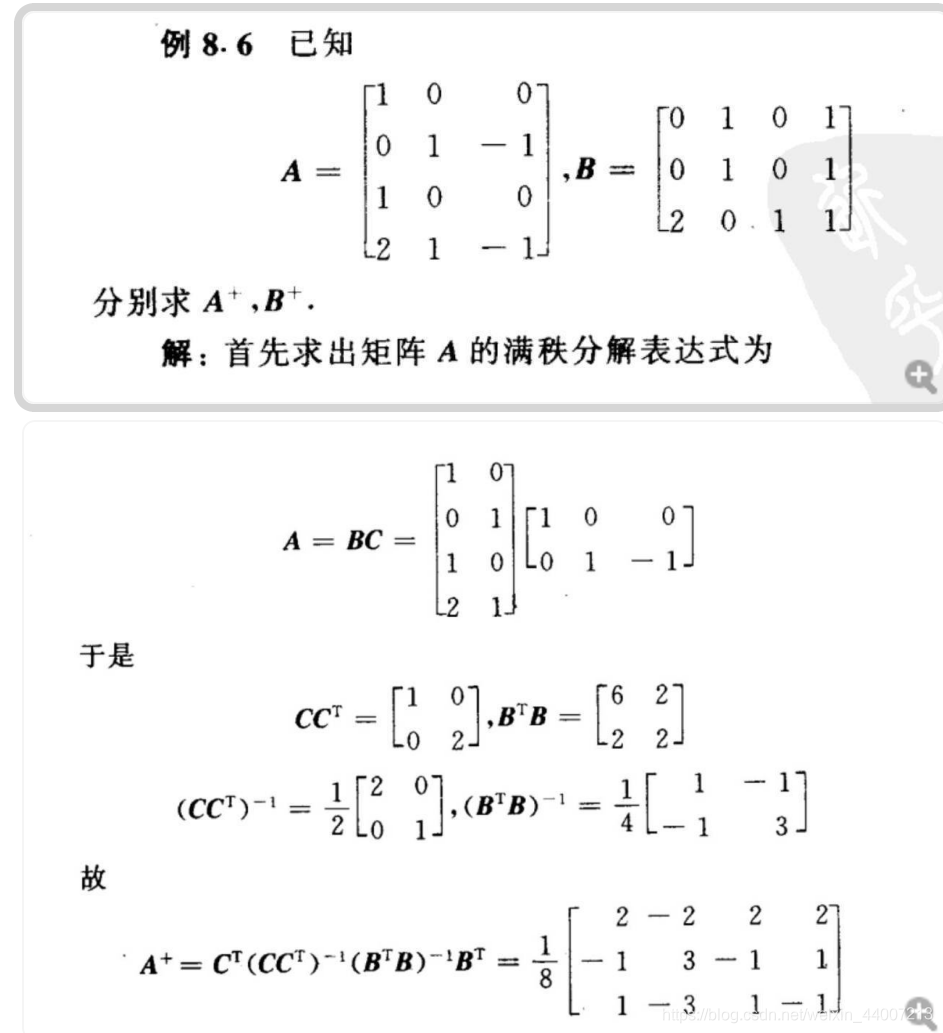
二、伪逆矩阵的求解

伪逆矩阵的求解主要依赖于奇异值分解（SVD）。对于非方阵或非满秩的矩阵，我们可以通过奇异值分解将其分解为三个部分：一个对角矩阵和两个正交矩阵。其中对角矩阵中的元素包含了原矩阵的主要信息，我们可以通过这个对角矩阵来求得伪逆矩阵。

三、伪逆矩阵的应用

1. 线性方程组的求解：当线性方程组的系数矩阵不是方阵或不是满秩时，我们可以利用伪逆矩阵来求解该方程组。
2. 最小二乘法：在数据拟合中，我们常常使用最小二乘法来找到最佳拟合直线或曲线。在这个过程中，我们也需要用到伪逆矩阵。
3. 图像处理：在图像处理中，常常需要对图像进行去噪、增强等操作，这些操作往往涉及到对图像矩阵的处理，而伪逆矩阵在图像处理中也有着广泛的应用。

四、伪逆矩阵的优缺点

优点：

1. 伪逆矩阵可以有效地解决非满秩矩阵的线性方程组求解问题。
2. 在最小二乘法中，伪逆矩阵可以帮助我们找到最佳拟合结果。
3. 在图像处理中，利用伪逆矩阵进行去噪、增强等操作可以提高图像的质量。

缺点：

1. 伪逆矩阵的计算可能会涉及到复杂的数学运算，计算量较大。
2. 伪逆矩阵并不总是唯一确定的，其解可能会存在多个。
3. 对于某些情况下的应用，可能并不完全符合我们的预期。

五、总结

总的来说，伪逆矩阵是一种在非满秩矩阵中描述线性方程组解的重要工具。通过奇异值分解等技术，我们可以有效地求解伪逆矩阵，并利用其在多个领域中进行应用。虽然伪逆矩阵有着一些优点和广泛的应用场景，但同时也需要注意其可能存在的缺点和局限性。在实际应用中，我们需要根据具体的问题和需求来选择是否使用伪逆矩阵，并注意其可能带来的影响和结果。