浮点运算

一、文章标题：浮点运算

二、文章内容：

浮点运算，顾名思义，是指涉及到小数点的运算。在计算机科学中，浮点数是一种非常重要的数据类型，用于表示实数。因此，浮点运算在各种科学计算、图形处理、金融计算等领域都有着广泛的应用。

1. 浮点数的概念和特点

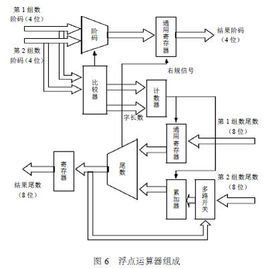
在计算机中，浮点数是由符号位、指数部分和尾数部分构成的。符号位用于表示数的正负，指数部分决定了数值的大小，而尾数部分则表示了数值的精度。与整数相比，浮点数能够表示更大范围和更精确的数值。

2. 浮点运算的基本操作

浮点运算包括加法、减法、乘法和除法等基本操作。这些操作都遵循数学上的基本原理，但考虑到计算机内部处理数据的方式和特点，浮点运算的实现方式与整数运算有所不同。

（1）加法与减法

浮点数的加法和减法需要先进行对阶操作，即对齐两个数的指数部分，使其能够进行相加或相减的运算。对阶完成后，将尾数部分进行加减运算，最后将结果组合成新的浮点数。

（2）乘法与除法

与加法和减法不同，浮点数的乘法和除法主要关注的是阶码的调整和尾数的乘除操作。乘法是将两个数的阶码相加，尾数相乘；而除法则是将两个数的阶码相减，然后以乘法的形式进行尾数的计算。

3. 浮点运算的精度与误差

由于计算机内部存储和计算的限制，浮点运算可能会出现精度损失和误差。这主要是由于计算机的二进制表示方式对于某些实数无法做到完全精确的表示。尽管如此，通过一些算法和技术手段（如舍入和截断），我们可以在一定程度上减小这些误差对计算结果的影响。

4. 浮点运算在计算机科学中的应用

浮点运算是计算机科学中不可或缺的一部分。在科学计算、图形处理、金融计算等领域，都需要用到大量的浮点运算来处理各种复杂的数学问题。此外，在人工智能、机器学习等领域，由于涉及到大量的数学模型和算法，因此对浮点运算的要求也极高。

综上所述，浮点运算是计算机科学中一个重要的概念和操作。掌握好浮点运算的相关知识和技术对于我们理解和应用计算机系统有着非常重要的意义。