高中数学残差公式

一、高中数学残差公式

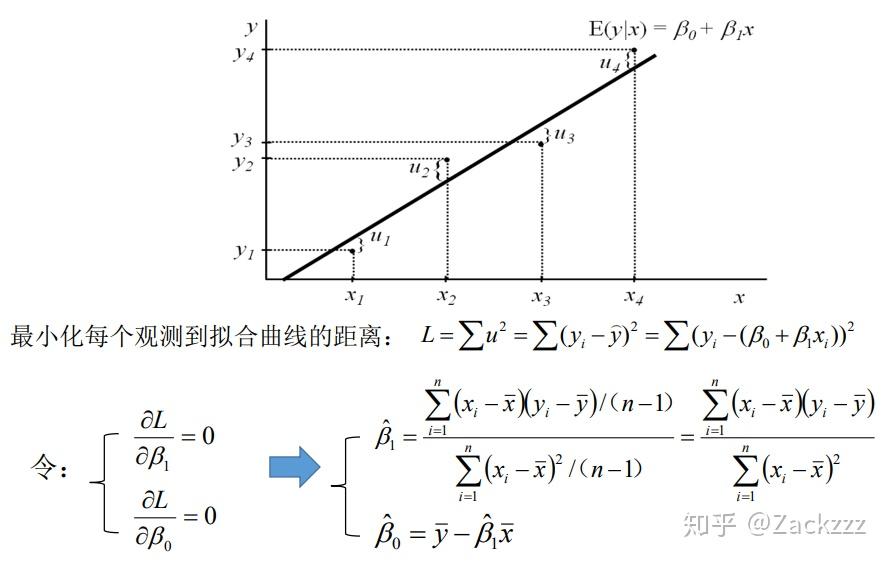
在统计学中，残差是一种用来描述预测值与实际观测值之间差距的量度。它不仅可以帮助我们理解模型与数据之间的适配程度，还是对模型质量进行评估的重要指标。特别是在高中数学学习中，理解残差及相关的计算公式，是提高数据分析能力的关键一步。

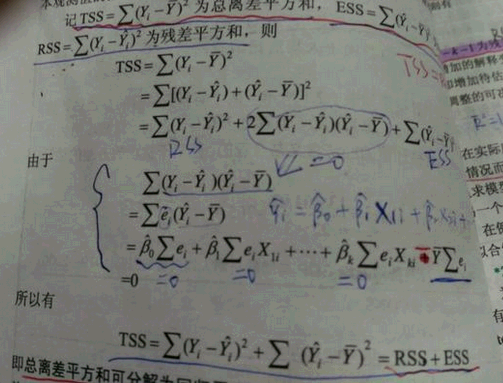
二、残差公式的概念及重要性

当我们用回归分析的方法去拟合一个模型时，通常会用到一个自变量（或多个自变量）与一个因变量之间的关系来描述。但在实际的数据分析中，由于各种因素的影响，模型的预测值往往与实际观测值存在差异，这种差异就是残差。

三、残差公式的具体形式

对于线性回归模型来说，残差通常表示为观测值与预测值之间的差值。假设我们有自变量X和因变量Y，并且用回归模型预测了Y的值，那么残差公式可以表示为：

残差 = 实际观测值 - 预测值

或者用数学符号表示为：e = y - y'（其中e代表残差，y代表实际观测值，y'代表预测值）。

值得注意的是，不同的模型可能会使用不同的残差计算公式。例如在时间序列分析中，常采用真实值与基于某种时间序列模型的预测值之差来计算残差。在回归分析中，不同的回归线计算方式也会导致不同的残差。因此在实际操作中需要根据具体情况来决定使用哪种计算方式。

四、残差的应用及作用

了解残差公式的目的不仅是用于计算差异值，更重要的是通过对残差的分析，可以更深入地了解模型的质量和数据的特征。例如，如果残差的分布呈现出某种模式或趋势，那么这可能意味着模型存在问题或数据存在异常。同时，通过对残差的统计分析，我们可以调整模型参数或选择更合适的模型来提高预测的准确性。

五、总结

总的来说，高中数学中的残差公式是数据分析的重要工具之一。它不仅可以帮助我们理解模型与数据之间的适配程度，还是对模型质量进行评估的重要指标。通过掌握残差公式的概念、形式和应用方法，我们可以更好地进行数据分析与建模工作。希望本文的介绍能够帮助大家更好地理解和应用残差公式。