并集的概念

并集的概念

一、引言

在数学领域中，集合论是一个重要的分支，它帮助我们理解和描述各种对象之间的关系和性质。并集是集合论中一种基本而重要的运算，它的定义和应用对于理解和研究集合的属性和问题具有重要意义。本文将深入解析并集的概念，通过理论解析和实际案例的探讨，以帮助读者全面理解这一概念。

二、并集的基本概念

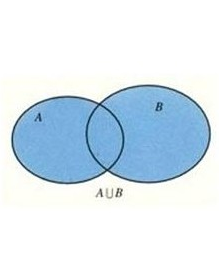
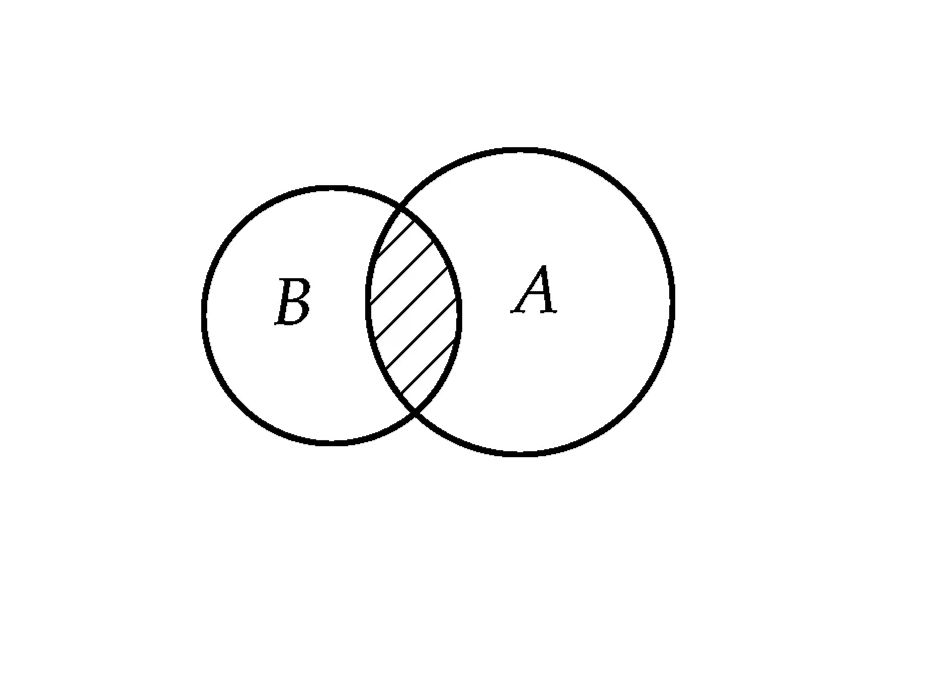
并集，顾名思义，就是将两个或多个集合中的所有元素合并成一个新的集合。具体来说，如果存在两个集合A和B，那么集合A和B的并集A∪B，就是由所有属于A或属于B的元素所组成的集合。

在数学符号中，我们使用“∪”来表示并集。例如，对于集合A={1, 2, 3}和集合B={3, 4, 5}，那么A∪B={1, 2, 3, 4, 5}。

三、并集的性质

并集具有以下性质：

1. 互不相交性：两个集合的并集是它们的元素相互独立，即两个集合的并集中没有重复的元素。

2. 可重复性：当两个集合中的元素相同或者存在公共元素时，这些元素在并集中只会出现一次。

3. 扩展性：对于任意数量的集合，它们的并集都是将所有这些集合中的元素合并成一个新的集合。

四、并集的实际应用

并集在数学、计算机科学、统计学等多个领域都有广泛的应用。例如，在计算机科学中，我们可以使用并集来描述两个数据集的合并；在统计学中，我们可以使用并集来描述两个数据集的联合分布等。

五、总结

通过本文的介绍，我们了解了并集的基本概念、性质以及应用场景。并集作为集合论中的一个重要概念，它帮助我们更好地理解和处理各种对象之间的关系和性质。同时，通过实际案例的探讨，我们可以更深入地理解并集的应用价值。希望本文能够帮助读者全面理解并掌握这一概念。