MOD运算

一、文章标题

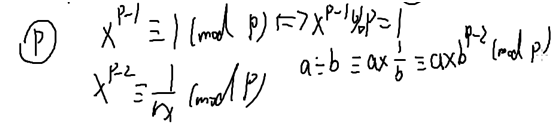
MOD运算

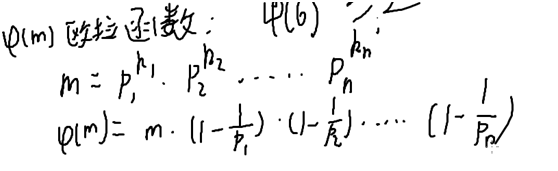
二、文章内容

在现代计算机编程和数学中，MOD运算是一个常见的概念。MOD运算又称取模运算，常用于判断一个数除以另一个数后的余数。在计算机科学中，MOD运算被广泛用于算法设计、数据加密、循环控制等场景。

1. MOD运算的定义

MOD运算的定义是：对于两个整数a和b（b不为0），取a除以b的余数。这个余数就是a对b的MOD值。例如，在十进制下，17除以5的余数是2，所以17 MOD 5的值为2。

2. MOD运算的规则

在MOD运算中，如果被除数大于除数，那么结果就是被除数除以除数的商的余数。如果被除数小于除数，那么结果就是被除数本身。此外，MOD运算还具有一些特殊的性质，如周期性、互逆性等。

3. MOD运算的应用

(1) 算法设计：在计算机编程中，MOD运算常常被用于算法设计。例如，在循环控制中，我们常常需要判断某个变量是否已经达到某个值，这时就可以使用MOD运算来判断。

(2) 数据加密：在密码学中，MOD运算也被广泛用于数据加密。通过对数据进行MOD运算，可以生成一个特定的结果，这个结果可以用于验证数据的完整性和真实性。

(3) 循环控制：在编程中，我们经常需要让程序按照一定的规律进行循环操作。这时，我们可以使用MOD运算来控制循环的次数和顺序。

4. MOD运算的注意事项

(1) 负数的MOD运算：在MOD运算中，如果被除数为负数，结果可能为正也可能为负。不同的编程语言有不同的规定。在多数情况下，MOD运算是基于“带余除法”进行的，余数会以绝对值的方式出现。因此在进行MOD运算时需要注意符号问题。

(2) 溢出问题：当被除数和除数都很大时，可能会发生溢出问题。这时需要使用大数库或者高精度的计算方法来进行处理。

以上就是关于MOD运算的基本概念和基本知识介绍。作为现代计算机科学中的基本操作之一，理解并掌握MOD运算对学习计算机科学具有重要意义。在实际应用中，我们应该注意MOD运算在不同场合下的不同规则和注意事项，灵活运用MOD运算来解决实际问题。