共轭梯度法

一、文章标题

共轭梯度法

二、文章内容

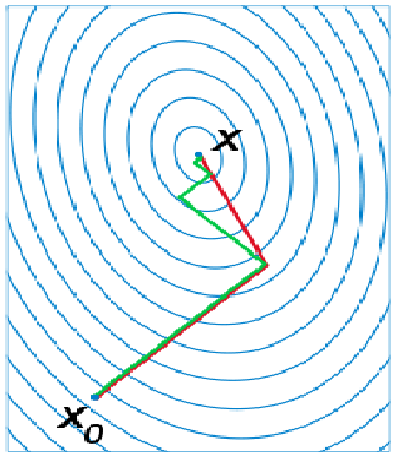
共轭梯度法是一种用于求解线性方程组的迭代方法，具有计算精度高、存储量小、收敛速度快等优点，广泛应用于科学计算和工程领域。

一、共轭梯度法的基本思想

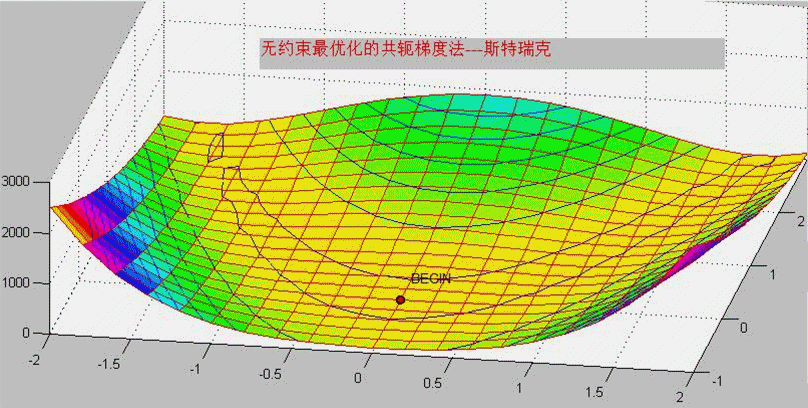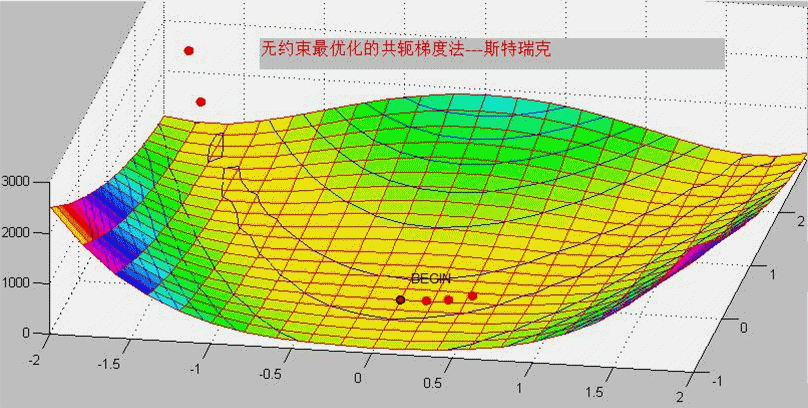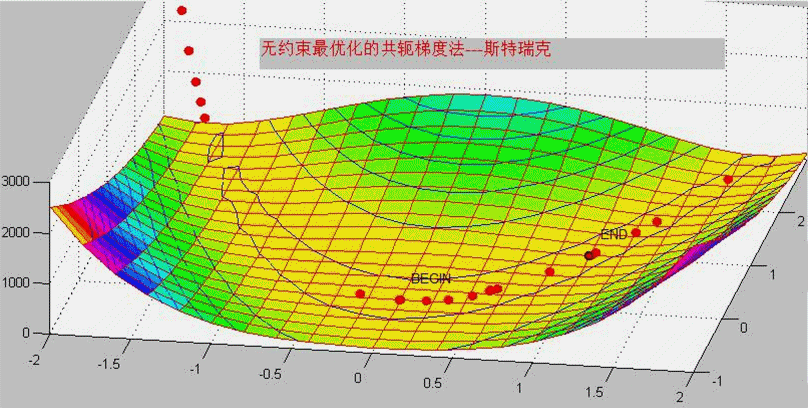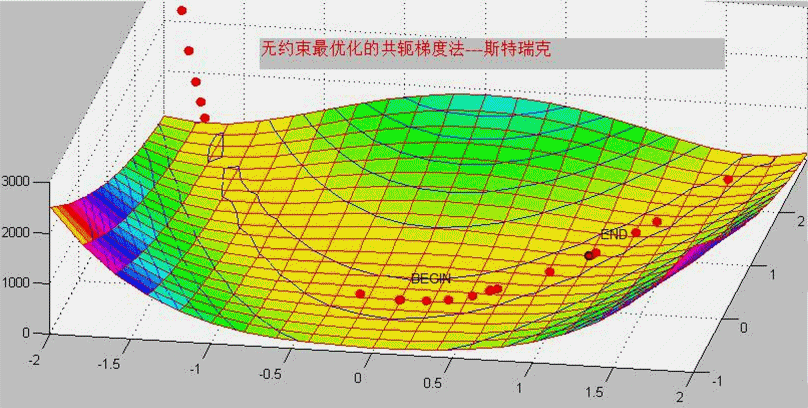
共轭梯度法的基本思想是利用梯度法中的负梯度方向进行迭代求解，通过构造一组共轭方向来提高收敛速度。该方法的核心在于利用线性方程组中矩阵的共轭性质，使得在每个迭代步骤中都能获得最优的搜索方向，从而加快收敛速度。

二、共轭梯度法的算法步骤

共轭梯度法的算法步骤主要包括以下几步：

1. 初始化：给定初始向量x(0)和误差限ε，以及线性方程组Ax=b中的系数矩阵A。

2. 计算残差r(0)：r(0)=b-Ax(0)，并将残差进行单位化。

3. 开始迭代：设当前迭代步为k，进行循环迭代直到满足停止准则（即|r(k)|<ε）。

4. 计算搜索方向p(k)：根据共轭性质计算搜索方向p(k)，使得p(k)与A的共轭方向正交。

5. 计算步长α(k)：通过求解一维搜索问题得到步长α(k)，使得函数值在p(k)方向上达到极小值。

6. 更新解向量x：x(k+1)=x(k)+α(k)p(k)。

7. 更新残差r(k+1)：r(k+1)=r(k)-α(k)Ap(k)。并再次单位化残差r(k+1)。

8. 检查停止准则：若|r(k+1)|<ε，则算法终止；否则返回第4步继续迭代。

三、共轭梯度法的应用场景

共轭梯度法广泛应用于各种科学计算和工程领域，如结构力学、电磁场计算、流体力学等。在结构力学中，共轭梯度法常用于求解线性弹性问题；在电磁场计算中，它被用来求解电磁场偏微分方程组；在流体力学中，它被用来求解流体动力学方程组等。此外，共轭梯度法还可以用于求解稀疏线性方程组，如稀疏矩阵的求逆问题等。

四、总结

共轭梯度法是一种高效的迭代方法，具有计算精度高、存储量小、收敛速度快等优点。它利用了线性方程组中矩阵的共轭性质，通过构造一组共轭方向来提高收敛速度。该算法广泛应用于各种科学计算和工程领域，具有广泛的应用前景和重要的理论价值。