补集的性质

补集的性质

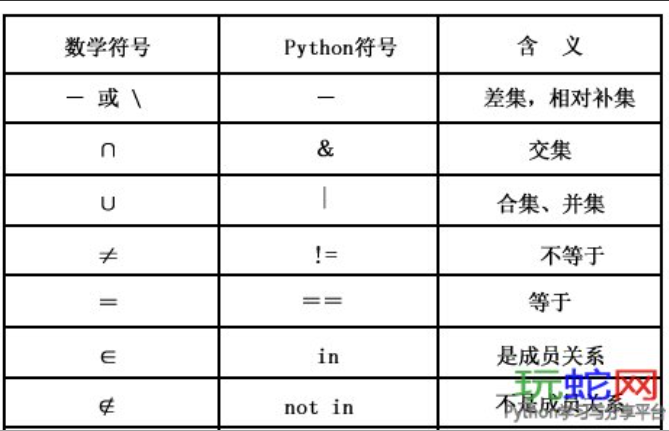
在数学中，补集是一个重要的概念，特别是在集合论中。补集的定义是：对于给定的集合A，所有不在A中的元素组成的集合，我们称之为A的补集。本文将详细探讨补集的性质。

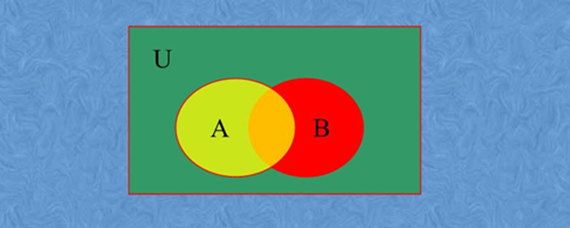
一、定义与基本性质

首先，补集是相对于某个特定集合而言的。对于任意一个集合A，其补集是全集中除去A的所有元素组成的集合。如果A和B是同一全集下的两个集合，那么B的补集就是全集中不属于B的所有元素组成的集合。

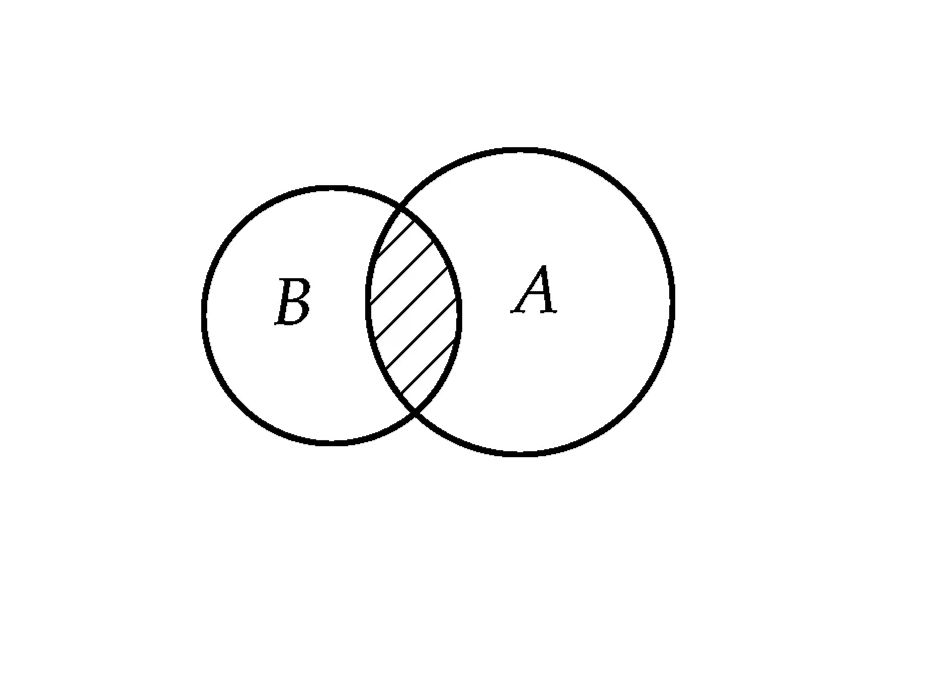
二、补集的运算性质

1. 互为补集：若A和B互为补集，则A与B的并集为全集，即A∪B=全集。
2. 补集的交集：对于任意两个集合A和B，它们的交集的补集是这两个集合的补集的并集的补集，即(A∩B)'=A'∪B'。
3. 补集的运算顺序：在处理涉及多个集合的补集问题时，运算顺序不影响结果。即无论先计算哪个集合的补集，最终的结果都是一样的。

三、补集的应用

补集在数学中有着广泛的应用。例如，在概率论中，一个事件的补集就是该事件不发生的所有可能性的集合。通过研究补集的性质，我们可以更好地理解集合之间的关系和运算。此外，在图论、逻辑学等领域，补集也有着重要的应用。

四、总结

补集是数学中一个重要的概念，它描述了相对于某个特定集合的所有不包含在该集合中的元素组成的集合。通过研究补集的性质和运算，我们可以更好地理解集合之间的关系和运算规则。同时，补集在概率论、图论、逻辑学等领域都有着广泛的应用。掌握补集的概念和性质，对于理解这些领域的基础知识具有重要的意义。

以上内容是对补集的基本定义和性质进行了简要的介绍和阐述，希望对大家有所帮助。