复数的绝对值

复数的绝对值

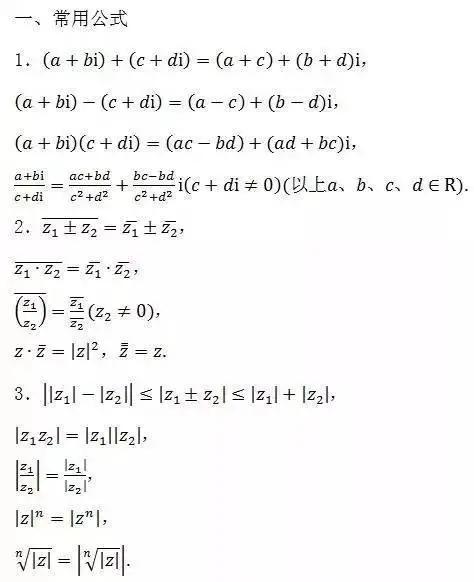
在数学中，复数是一种重要的概念，它扩展了实数系统的范围，并允许我们解决更复杂的问题。其中，复数的绝对值是复数的一个重要属性，对于复数的研究有着至关重要的意义。本文将详细介绍复数的绝对值的概念、性质和计算方法。

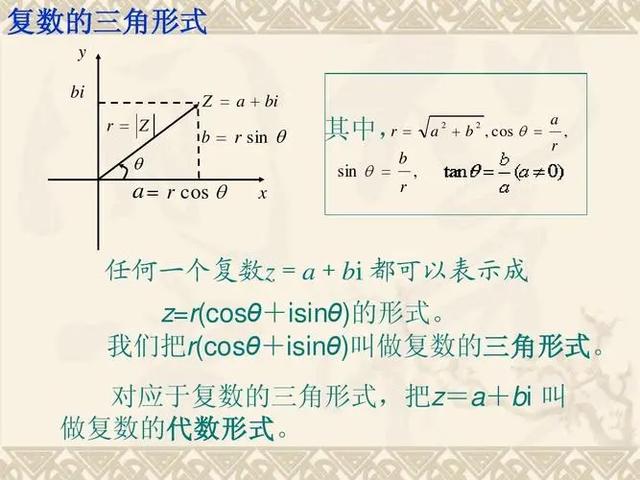
一、复数绝对值的概念

复数是由实部和虚部组成的数，一般表示为a+bi的形式，其中a是实部，b是虚部。复数的绝对值，就是将这个复数视为一个向量在复平面上所表示的模长。它的大小与该向量在平面上的长度相对应，且是一个非负的实数。

二、复数绝对值的性质

1. 任何复数的绝对值都是非负的。
2. 如果一个复数的绝对值为0，那么这个复数就是实数0。
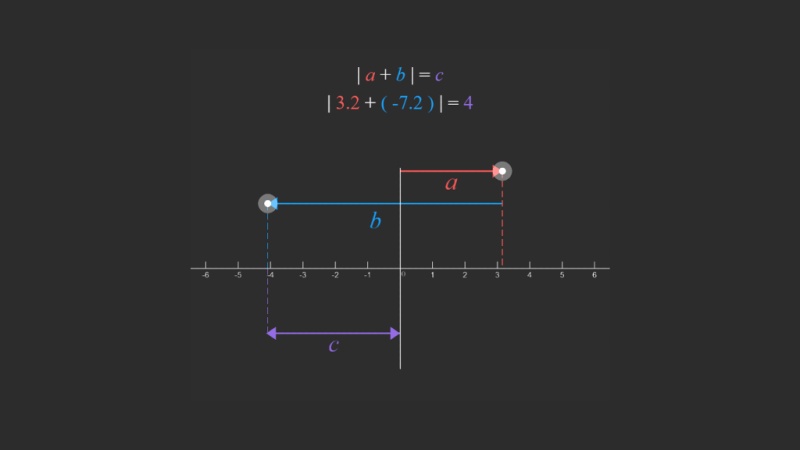
3. 两个复数的和（或差）的绝对值等于这两个复数绝对值的和（或差）。
4. 复数的绝对值与它的共轭复数的绝对值相等。

三、复数绝对值的计算方法

对于任意一个复数z=a+bi，其绝对值可以按照以下公式计算：|z| = sqrt(a^2 + b^2)。也就是说，将复数的实部和虚部平方后相加，然后开方即可得到其绝对值。

四、计算示例

以复数z=3+4i为例，它的实部a=3，虚部b=4。根据公式，我们可以计算出它的绝对值为：|z| = sqrt(3^2 + 4^2) = sqrt(9 + 16) = sqrt(25) = 5。因此，该复数的绝对值为5。

五、结论

复数的绝对值是复数的一个重要属性，它描述了复数在复平面上的长度。通过计算复数的绝对值，我们可以更好地理解复数的性质和特点，从而更好地应用它们解决实际问题。同时，掌握复数的绝对值的计算方法也是数学学习中必不可少的一部分。