什么是补集

一、文章标题：什么是补集

二、文章内容

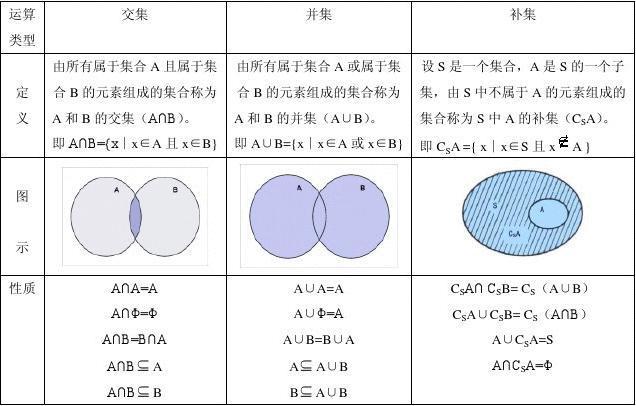
在数学中，补集是一个重要的概念，它涉及到集合论的范畴。补集是指在一个特定的集合中，所有不属于某个子集的元素所组成的集合。简单来说，一个集合的补集就是在这个集合的范围内，除去某个特定子集后剩下的所有元素。

1. 补集的定义

设S是一个集合，A是S的一个子集，那么A在S中的补集，记作S减A，就是S中所有不属于A的元素构成的集合。也就是说，S减A包含的是所有在S中但不在A中的元素。

2. 补集的运算

补集的运算主要包括与运算、差运算等。例如，设两个集合A和B都属于同一个更大的集合S，那么A相对于B的补集，就意味着是在A和B之外的集合元素组成的子集。如果我们需要做减法运算（A减B），结果就会是一个包含了属于A但不属于B的所有元素的集合。

3. 补集的应用

补集在数学中有着广泛的应用。在逻辑推理、集合运算、计算机科学等领域都有重要的作用。例如，在计算机科学中，补集的概念被用来描述数据结构中的某些操作。在一个有限集合中，如果一个元素没有被包含在某个子集中，那么它就会成为该子集的补集的一部分。在数据库查询语言中，也常常会涉及到对数据集合的补集操作。

4. 补集的例子

假设有一个班级的所有学生组成一个集合S，而某次考试的及格学生组成一个子集A。那么S中减去A后的元素就组成了A的补集，也就是不及格学生的集合。这就是一个典型的补集在实际生活中的运用。

总的来说，补集是集合论中的一个重要概念，它对于理解集合的运算和关系有着重要的作用。在数学学习中掌握好补集的概念及其运算方法是非常重要的。而在实际应用中，我们也需要利用补集来更好地理解、分析和处理实际问题。