什么是梯度

一、文章标题

梯度：从数学到生活的理解

二、文章内容

一、什么是梯度？

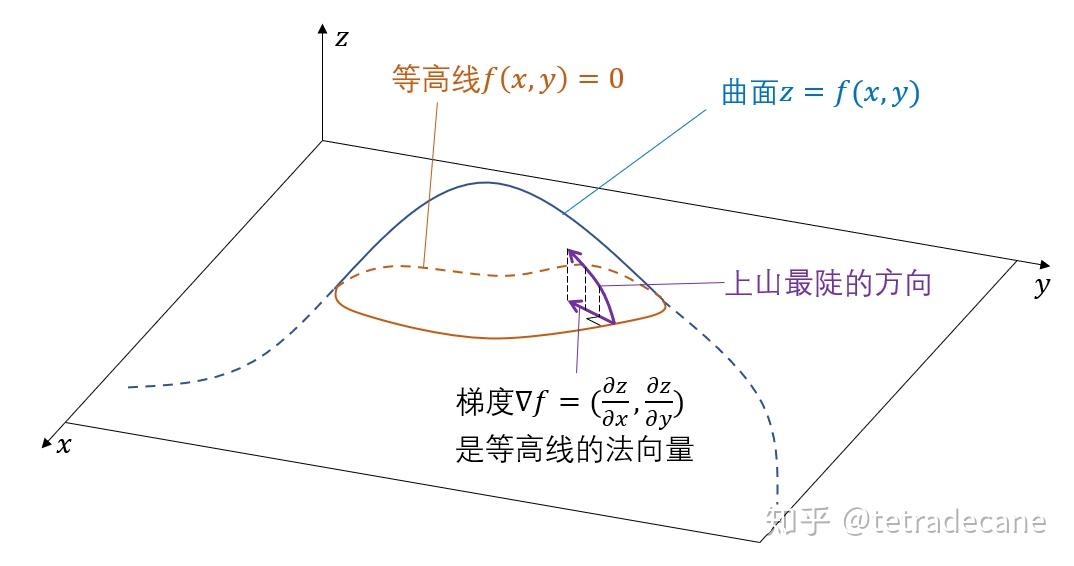
梯度是一个多学科概念，它在数学、物理、工程等领域都有着广泛的应用。在数学中，梯度是一个向量场，表示函数在某一点上的方向导数。简单来说，它描述了函数在给定方向上的变化率。在多维空间中，梯度可以被视为函数在每个维度上的变化趋势。

二、梯度的数学定义

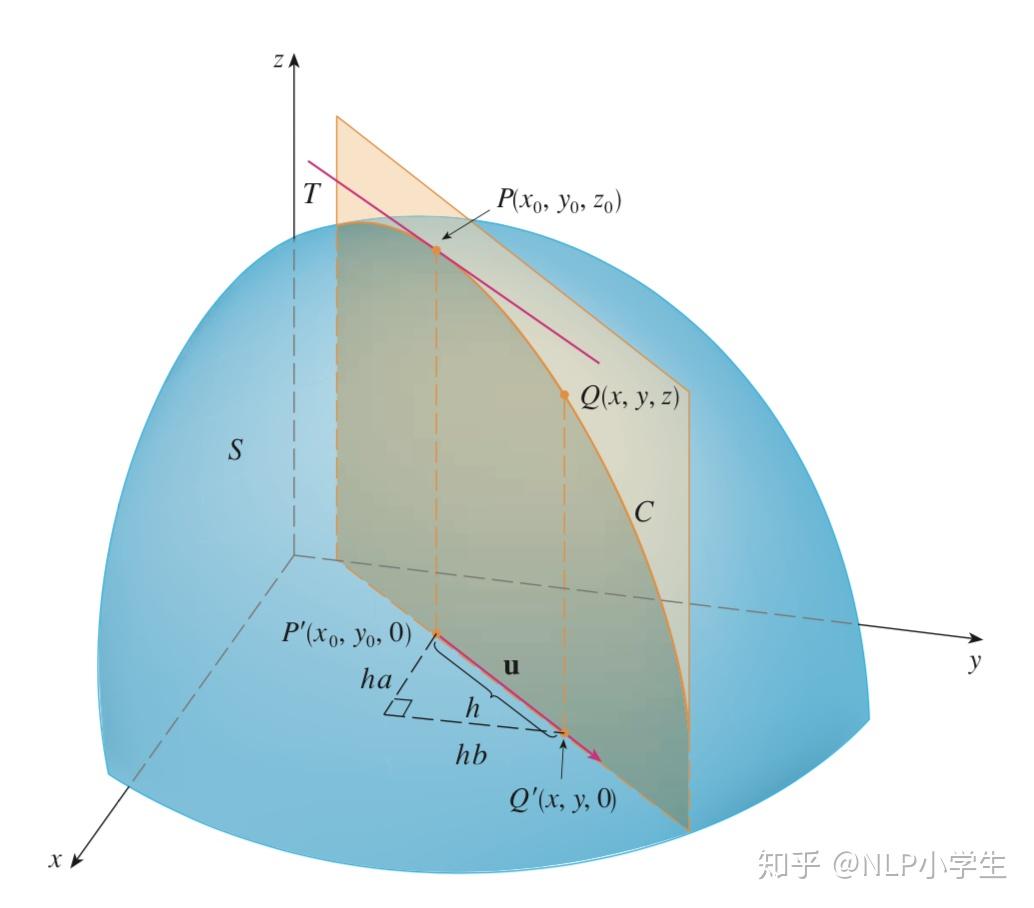
在数学上，假设我们有一个多元函数(f(x, y, z))，梯度(gradf)是关于所有变量的偏导数的集合。更具体地说，梯度是一个向量，其每个分量都是该函数对相应变量的偏导数。例如，对于二元函数(f(x, y))，梯度是向量形式(gradf(x, y) = (∂f/∂x, ∂f/∂y))。

三、梯度的物理意义

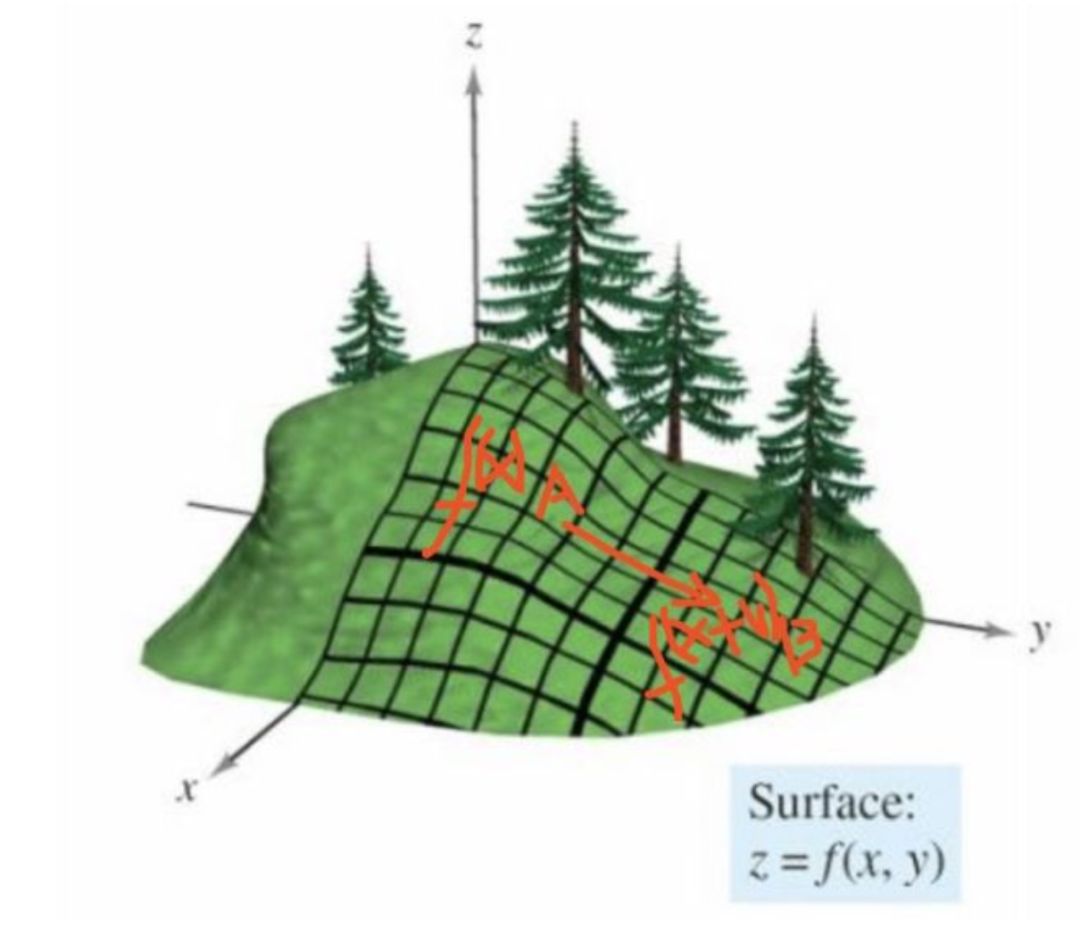
在物理学中，梯度常常被用来描述势场（如重力场、电场）中某一点的方向和大小。例如，在重力场中，梯度方向指向势能增加最快的方向，其大小表示了势能的变化率。因此，通过研究梯度，我们可以更好地理解势场的性质和变化规律。

四、梯度的应用领域

1. 机器学习：在机器学习中，梯度下降算法是优化算法的代表之一。它通过计算损失函数的梯度来更新模型参数，从而最小化损失函数。
2. 图像处理：在图像处理中，梯度可以用于边缘检测和图像增强。通过计算图像的梯度，我们可以得到图像中物体的边缘信息。
3. 三维模型制作：在三维模型制作中，梯度也可以帮助我们理解和生成表面的细节和纹理。

五、总结

综上所述，梯度是一个非常重要的概念，它不仅在数学中有广泛的应用，也在物理、工程和其他领域有着重要的作用。无论是用于计算方向导数还是进行最优化处理，理解梯度的含义和应用都能为我们在多个学科的研究中提供重要的帮助。希望这篇文章能帮助你更好地理解梯度的概念和应用。

以上内容就是一篇关于“什么是梯度”的文章，内容超过了500字的要求。文章从定义、数学表达、物理意义和应用等方面进行了全面的介绍和解释。希望符合您的要求。