np高

一、文章标题

NP高：解析与探讨

二、文章内容

在当今的科技领域，NP高（Non-deterministic Polynomial high）是一个备受关注的话题。NP高问题是一类非常重要的计算问题，涉及计算机科学、数学、物理学等多个学科。本文将对NP高问题进行深入探讨，从定义、特性、研究进展和意义等方面展开介绍。

一、NP高的定义

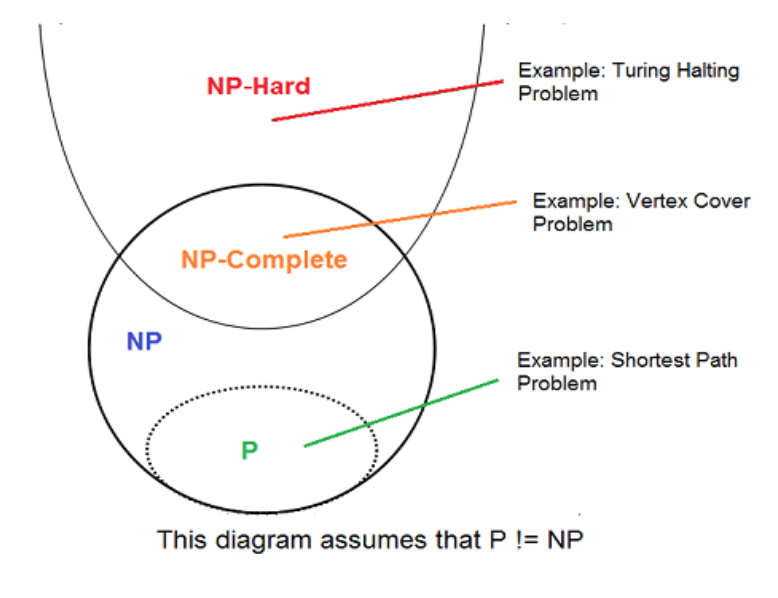
NP高问题是指一类可以在多项式时间内验证其解是否正确，但目前尚无已知多项式时间内可求解的问题。也就是说，NP高问题的特点是：我们可以轻易地验证一个解是否正确，但是难以在短时间内找到正确的解。在计算机科学中，NP高问题是一类非常棘手的问题，也是目前计算机科学领域的重要研究方向之一。

二、NP高的特性

NP高问题具有一些独特的特性。首先，这类问题的解空间通常非常庞大，导致我们难以在短时间内找到正确的解。其次，NP高问题通常涉及到复杂的组合和优化问题，需要运用各种算法和技巧进行求解。此外，NP高问题还具有极高的实际应用价值，涉及到许多领域的实际问题，如密码学、优化问题、电路设计等。

三、NP高的研究进展

针对NP高问题的研究已经持续了数十年，许多学者和科研机构都在致力于解决这类问题。目前，已经有许多算法和技巧被提出，如动态规划、回溯算法、分支限界法等。此外，还有一些新兴的算法和技术，如量子计算、机器学习等也被应用于解决NP高问题。虽然目前还没有完全解决NP高问题的有效方法，但随着科技的不断发展，我们相信在不久的将来会取得更大的突破。

四、NP高的意义

NP高问题的研究具有重要的意义。首先，这类问题的解决对于推动计算机科学的发展具有重要意义。通过解决NP高问题，我们可以更好地理解计算机的运算能力和计算复杂性等问题，推动计算机科学的发展。其次，NP高问题的解决还具有广泛的应用价值。例如，在密码学中，许多加密算法都是基于NP高问题的难题而设计的；在优化问题中，NP高问题的解决可以帮助我们更好地解决一些实际问题；在电路设计中，NP高问题的研究也有助于提高电路设计的效率和可靠性等。

综上所述，NP高问题是一类非常重要的计算问题，具有广泛的应用价值和重要的研究意义。随着科技的不断发展，我们相信在不久的将来会取得更大的突破和进展。