arccot图像

arccot图像的解析

一、引言

在数学领域，反三角函数是重要的工具之一，而arccot（反余切）函数就是其中之一。它通常用于计算角度值，尤其在处理某些复杂问题的时候有着不可替代的作用。这篇文章将为大家介绍arccot函数的图像和特点。

二、arccot函数的定义

首先，我们先了解下arccot函数的定义。arccot函数是余切函数的反函数，其定义域为全体实数R，值域为开区间(0, π)。arccot函数的基本性质决定了其图像在坐标系中的分布。

三、arccot函数的图像

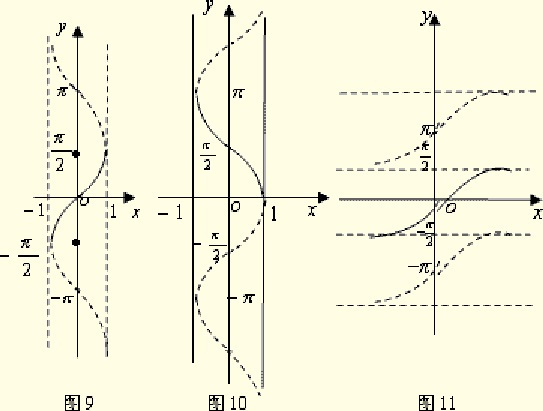
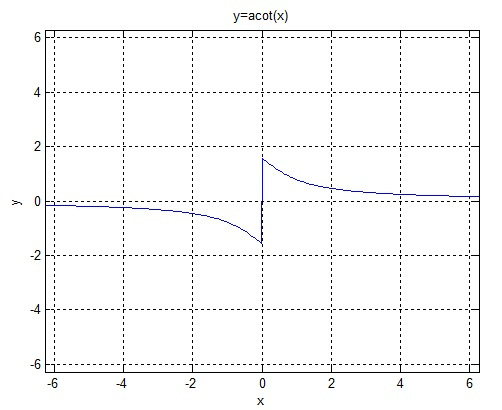
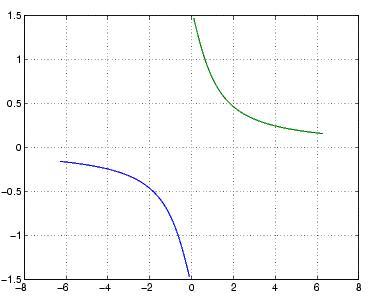
在平面直角坐标系中，arccot函数的图像是一个曲线。我们可以看到，在第一象限和第三象限中，arccot函数的图像分别与x轴和y轴呈一定的角度关系。

具体来说，arccot函数的图像是一条从第二象限延伸到第四象限的曲线，并且随着x值的增大，曲线从第三象限向第一象限延伸。这条曲线上的每一点都表示着某个角度值，这是由于arccot函数具有从余切值转换到角度值的特性。

在具体绘制时，我们可以在平面直角坐标系中绘制出x轴和y轴，然后根据arccot函数的性质和定义，在合适的角度上绘制出相应的曲线。这样我们就可以清晰地看到arccot函数的图像了。

四、arccot函数图像的特点

arccot函数图像的特点主要体现在它的形状和位置上。它是一个在第二、三、四象限内的单调递增曲线，而在第一象限内则是单调递减的。同时，由于它的定义域和值域都是实数集的一部分，所以它的图像没有固定的终止点或起始点，而是一直连续延伸的。

五、结论

综上所述，我们详细地解析了arccot函数的定义和它的图像。理解其特点和形状可以帮助我们更好地掌握和应用这一反三角函数工具。当然，要真正掌握并运用好这个工具，还需要我们不断练习和深化理解。

以上内容仅作为参考，实际编写时可以根据需要进行更深入的探讨和解释。希望这篇文章能对你有所帮助！