ttest

一、文章标题

ttest：从统计学到数据分析

二、文章内容

ttest是一种常见的统计方法，被广泛应用于数据分析和科研实验中。在本文中，我们将介绍ttest的原理、应用场景和具体实现方法。

一、ttest的原理

ttest是一种基于t分布的统计检验方法，用于比较两组或多组数据之间的差异是否显著。在ttest中，我们通常会对数据进行假设检验，即根据样本数据推断总体数据的特征。ttest的原理主要基于以下假设：

1. 两组数据的样本量应该相近；
2. 两组数据都应该服从正态分布；
3. 两组数据的方差应该相等。

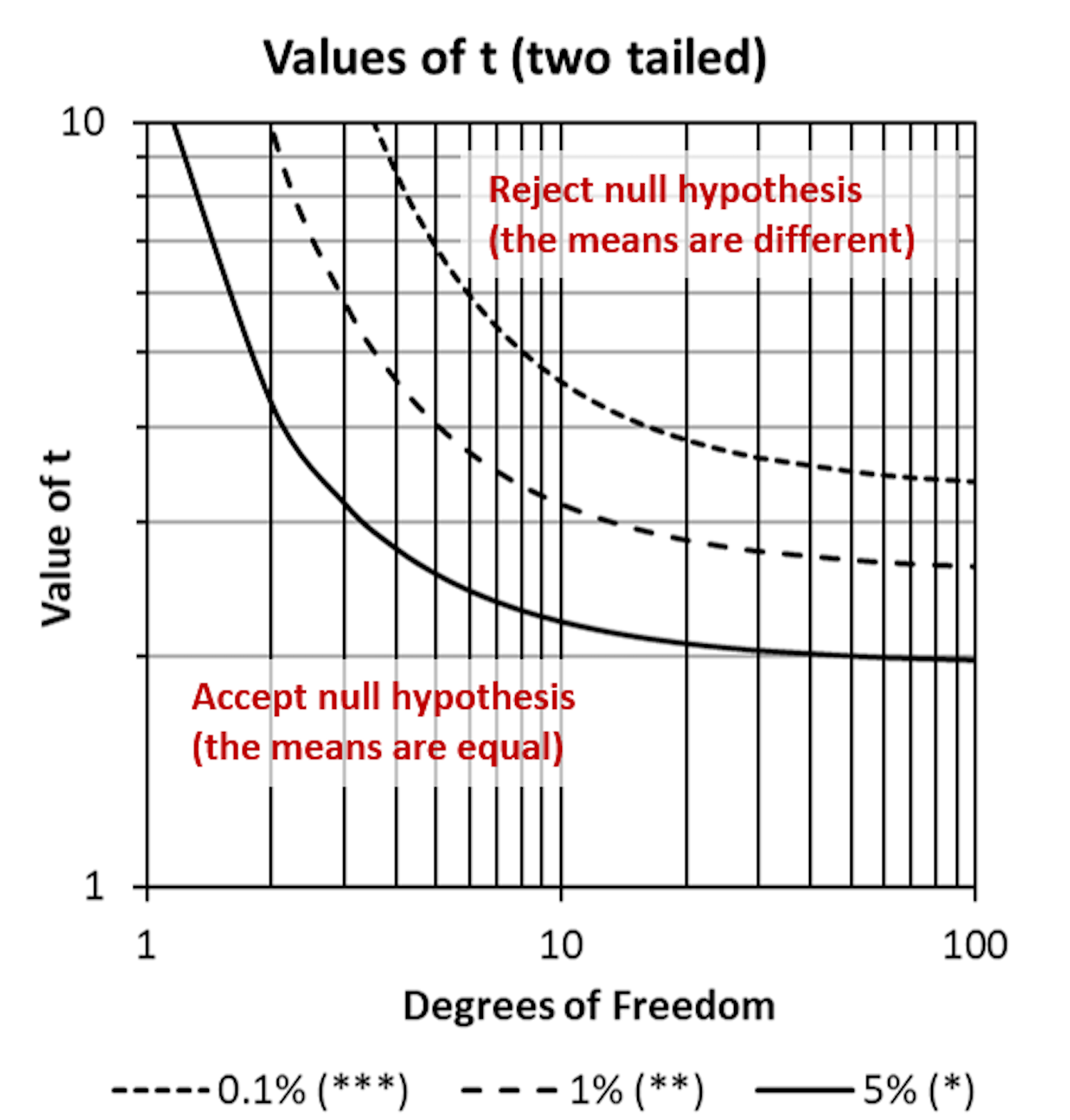
在满足以上假设的前提下，我们可以通过计算t值和p值来判断两组数据之间的差异是否显著。其中，t值表示两组数据的平均值差异与总体标准误差的比值，p值则表示观察到的数据差异在假设为真的情况下出现的概率。

二、ttest的应用场景

ttest在数据分析和科研实验中有着广泛的应用场景。例如，我们可以使用ttest来比较两个不同组之间的平均值是否存在显著差异，或者比较同一组在不同时间点的平均值是否存在显著变化。此外，ttest还可以用于检验某个变量的变化是否与另一个变量有关联等。

三、ttest的具体实现方法

在Excel或SPSS等统计软件中，我们可以使用ttest来对数据进行处理和分析。具体实现方法如下：

1. 导入数据：将要分析的数据导入到统计软件中；
2. 选择ttest：在统计软件中选择ttest功能；
3. 设置假设检验条件：根据实际情况设置假设检验条件，如两组数据的样本量、是否服从正态分布等；
4. 计算t值和p值：根据设置的条件，计算t值和p值；
5. 判断结果：根据p值的大小来判断两组数据之间的差异是否显著。

四、注意事项

在进行ttest时，需要注意以下几点：

1. 数据需要满足ttest的假设条件；
2. 需要根据实际情况选择适当的ttest类型，如单样本t检验、双样本t检验等；
3. ttest的结果只能作为参考，不能作为绝对结论；
4. 需要结合其他统计方法和数据分析技术来综合分析数据。

总之，ttest是一种常用的统计方法，可以帮助我们分析和比较数据之间的差异是否显著。在进行数据分析时，我们可以根据实际情况选择适当的ttest类型和假设检验条件来处理和分析数据。