ols回归模型
一、Ols回归模型简介
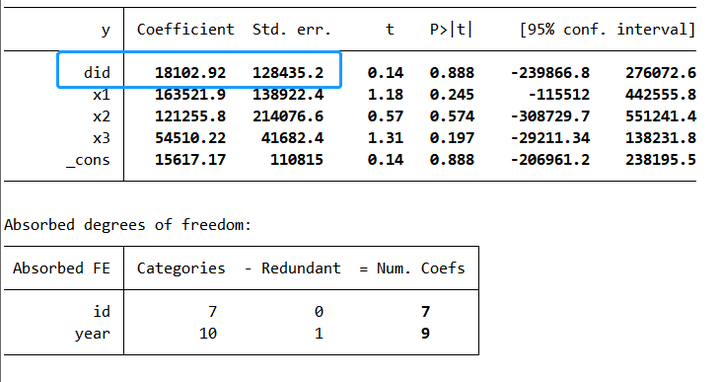
Ols回归模型,即最小二乘法回归模型,是统计学中常用的一种预测和分析的方法。其核心思想是通过最小化误差的平方和来寻找最佳函数匹配,使得预测值与实际值之间的差距最小。Ols回归模型广泛应用于各种领域,包括经济学、生物学、社会学等,用于揭示变量之间的关系,进行预测和决策。
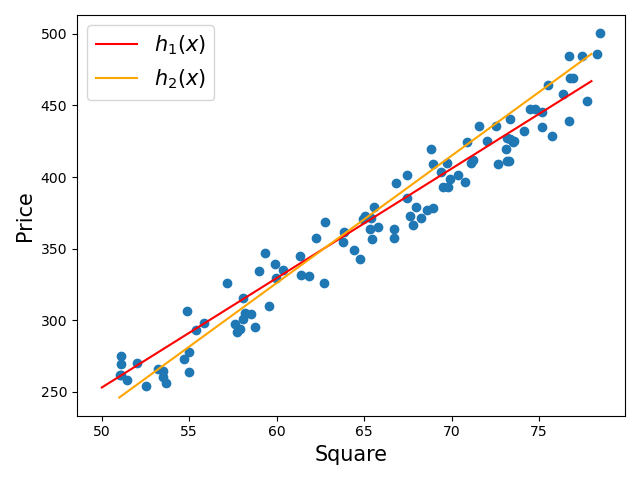
二、Ols回归模型的基本原理
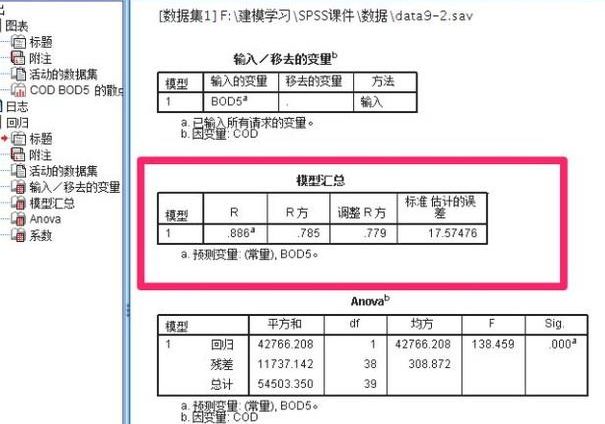
Ols回归模型的基本原理是利用观测数据,通过最小化误差的平方和来求解最佳参数。具体来说,它通过建立因变量与自变量之间的线性关系模型,来描述因变量如何被自变量所影响。在模型中,我们通常使用最小二乘法来估计未知的参数,使得模型预测的因变量值与实际观测值的误差平方和达到最小。
三、Ols回归模型的步骤
-
确定自变量和因变量:根据研究目的和数据特点,选择合适的自变量和因变量。
-
建立模型:根据自变量和因变量的关系,建立线性回归模型。
-
参数估计:利用最小二乘法估计模型的参数,即回归系数的值。
-
模型检验:对模型进行统计检验,检验其是否符合观测数据的分布和关系。
-
模型应用:将模型应用于实际问题中,进行预测和分析。
四、Ols回归模型的优点和局限性
优点:
-
简单易懂:Ols回归模型是一种简单的线性模型,易于理解和操作。
-
适用范围广:Ols回归模型适用于各种领域的数据分析,可以揭示变量之间的关系。
-
预测能力强:Ols回归模型能够根据自变量的值预测因变量的值,具有一定的预测能力。
局限性:
-
线性假设:Ols回归模型假设因变量与自变量之间存在线性关系,如果这种关系不成立,则模型的预测能力会受到影响。
-
无法处理非线性关系:Ols回归模型只能处理线性关系,对于非线性关系需要采用其他方法进行处理。
-
忽略其他因素:Ols回归模型只考虑了自变量对因变量的影响,忽略了其他可能影响因变量的因素。
五、总结
Ols回归模型是一种常用的统计分析方法,具有简单易懂、适用范围广、预测能力强等优点。但是,它也存在一些局限性,如线性假设、无法处理非线性关系和忽略其他因素等。因此,在使用Ols回归模型时,需要根据具体情况进行选择和应用,注意其适用条件和限制。同时,还需要对模型进行统计检验和验证,以确保其可靠性和有效性。

