样条插值

一、样条插值

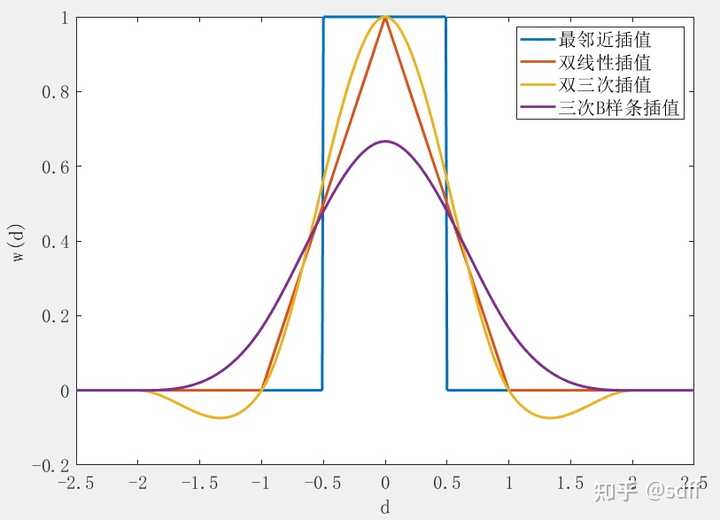
引言

在数据处理与数值分析中，样条插值是一种重要的数学工具。它通过对已知的离散数据进行数学建模，以达到在未知区域进行数据预测或近似表示的目的。样条插值在众多领域有着广泛的应用，如物理模拟、图像处理、计算机辅助设计等。

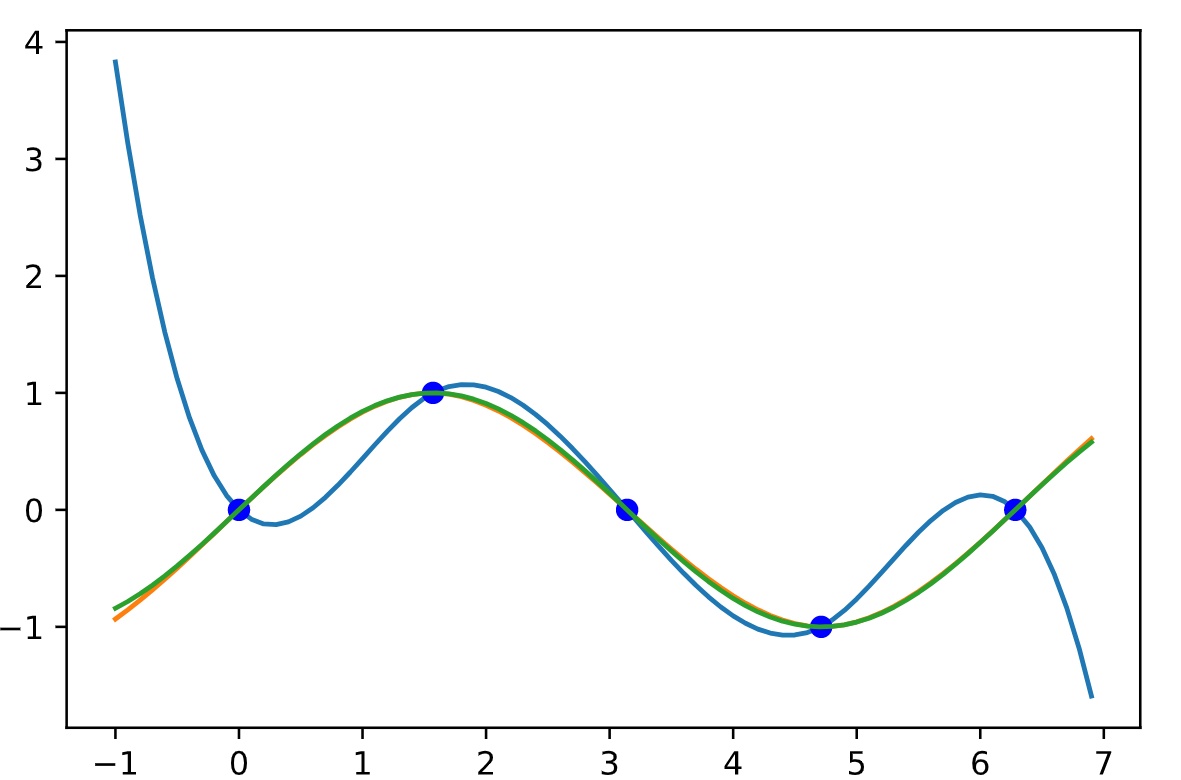
一、样条插值的基本概念

样条插值的核心思想是利用一组光滑的曲线来连接离散的数据点。这些曲线被称为样条，其特点是具有一定的连续性和平滑性。通过这种方式，我们可以利用已知的数据点来构建一个近似于实际数据的模型，并在此模型上进行进一步的分析或预测。

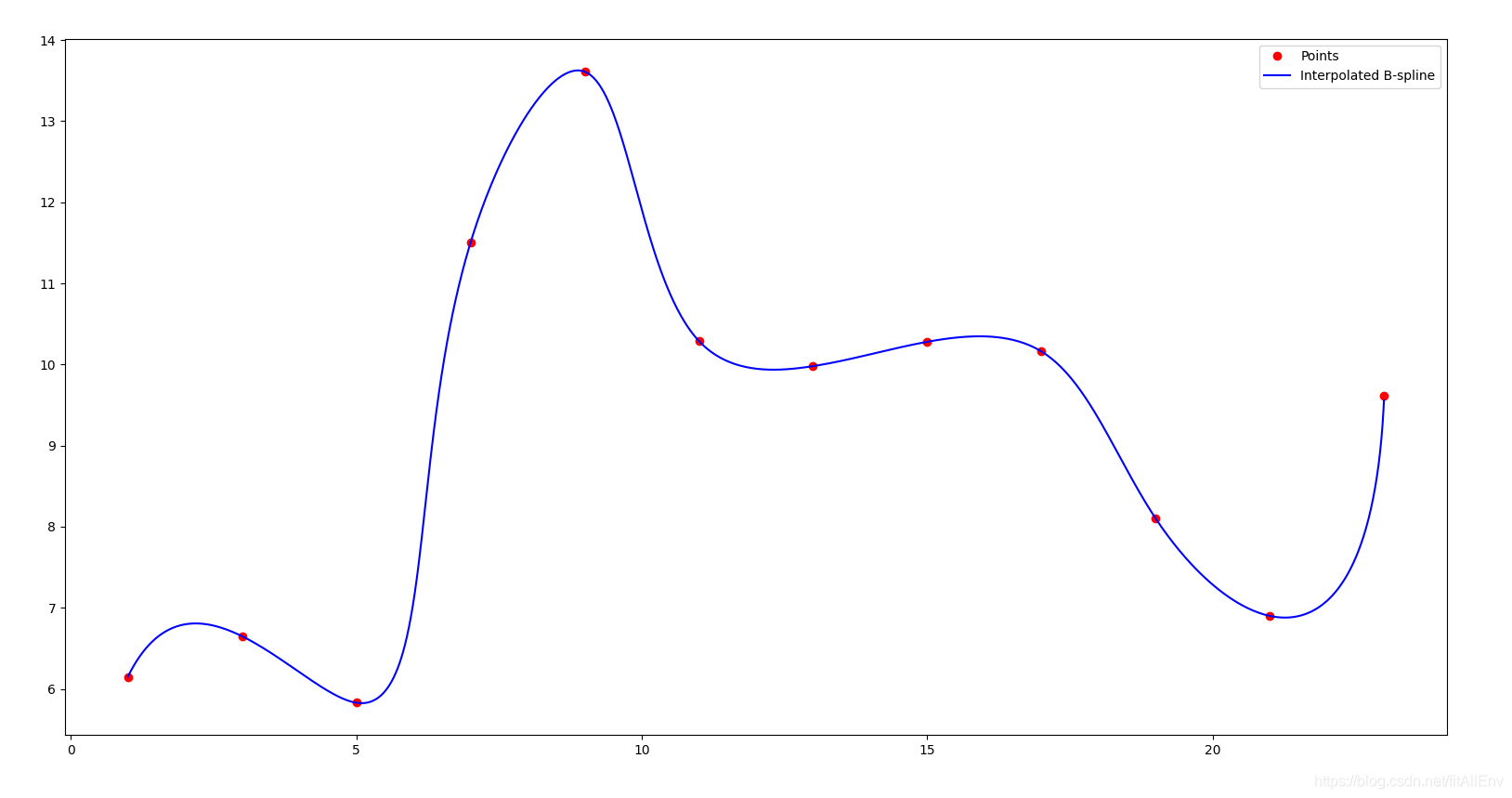
二、样条插值的方法

样条插值的方法多种多样，其中最为常用的是B样条插值法。B样条是一种分段多项式，它在连接处具有特定的连续性和平滑性。通过对这些样条函数进行选择和调整，可以找到一种能够最佳地近似实际数据的模型。此外，还有其他的插值方法，如多项式插值、拉格朗日插值等。

三、样条插值的应用

1. 物理模拟：在物理模拟中，样条插值常被用于构建物体的表面模型，以实现更加逼真的渲染效果。
2. 图像处理：在图像处理中，样条插值常被用于图像的缩放和旋转等操作，以保持图像的平滑性和连续性。
3. 计算机辅助设计：在计算机辅助设计中，样条插值可用于建立精确的几何模型，以便于后续的设计和加工。

四、样条插值的优缺点

优点：

1. 可以提供连续且平滑的模型；
2. 可以根据需求调整模型的复杂度和精度；
3. 在某些情况下具有较高的预测精度。

缺点：

1. 对初始数据的依赖性较大；
2. 在某些情况下可能存在过拟合或欠拟合的问题；
3. 计算量可能较大，特别是在处理大规模数据时。

五、结论

样条插值作为一种重要的数学工具，在数据处理和数值分析中发挥着重要作用。通过合理的选择和调整，可以有效地解决各种实际问题。然而，也需要注意其潜在的局限性和挑战，如数据的依赖性和计算复杂性等。因此，在使用样条插值时，需要结合具体的应用场景和需求进行综合评估和选择。