数学e

数学e的魅力与奥秘

在数学的浩瀚星空中，有一个特殊的符号，它就是数学中的基础常数——e。它虽然看似简单，却蕴含着深奥的数学原理和广泛的应用。

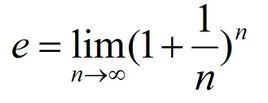
一、什么是数学e？

e是自然对数的底数，大约等于2.71828。它最初由数学家约翰·纳皮尔在研究复利增长的过程中发现，被广泛运用于概率论、统计学、微积分等领域。

二、e的数学性质

e的数学性质十分丰富，包括它的导数、微积分等特性。例如，e的指数函数在数学上具有独特的性质，它是一个无界的增长函数，可以用来描述许多自然现象的增长趋势。

三、e在现实生活中的应用

1. 复利计算：在金融领域，e被广泛应用于复利计算中，它能够精确地计算出资金随时间增长的情况。

2. 放射性物质衰变：在放射性物质衰变的研究中，e也被广泛应用。例如，在核物理中，使用e可以精确地计算出放射性物质衰变的概率。

3. 概率论与统计学：在概率论和统计学中，e也扮演着重要的角色。例如，在计算某些概率分布时，需要使用到e的指数函数。

四、e的神秘之处

除了上述的应用外，e还具有一些神秘的特性。例如，e的某些幂次方具有特殊的序列规律，如e的平方根的十进制表示是一个无限不循环的小数，但它的前几位数字却呈现出一种奇妙的规律性。此外，e还与许多其他数学常数有着密切的联系，如圆周率π等。

五、结语

综上所述，数学e不仅是一个数学常数，更是一种思考问题的方式。它在许多领域都发挥着重要的作用，同时也展示了数学的奇妙与魅力。通过学习和研究e，我们可以更深入地理解数学的奥妙和美丽。

以上内容仅为简述数学e的魅力与奥秘，如需更深入地了解其相关知识，建议查阅相关数学书籍或文献。