标题：正交阵

在数学中，正交阵（或称正交矩阵）是一种非常特殊的矩阵。它的每一个列（或行）都作为一个向量空间里的基向量，且这些基向量之间是正交的。正交阵在许多领域都有广泛的应用，包括线性代数、量子力学、计算机视觉等。

一、正交阵的定义

正交阵是一个方阵，其转置矩阵与它的乘积等于单位矩阵。也就是说，如果A是一个n阶正交阵，那么AA^T = E（E为n阶单位矩阵）。同时，A的每一列（或行）都是单位向量，且任意两个不同的列（或行）之间的点积都为0。

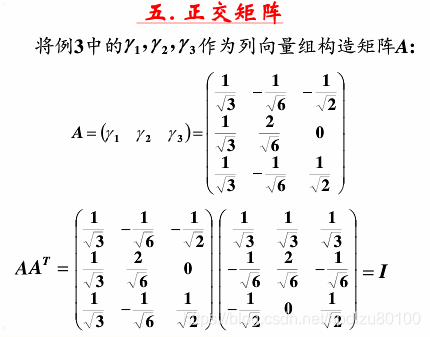
二、正交阵的性质

1. 列（或行）正交：正交阵的每一列（或行）都是相互正交的。这意味着任意两个不同的列（或行）之间的点积都为0。
2. 模长为1：正交阵的每一列（或行）的模长都为1，即每个向量都是单位向量。
3. 保持向量的长度不变：如果A是一个正交阵，且A的输入是n维欧几里得空间中的任意向量，那么输出向量的长度和原向量相同。

三、正交阵的运算性质

在计算中，我们可以通过使用正交阵的特性进行快速且精确的矩阵计算。由于正交阵的性质，例如它们的转置矩阵与原矩阵之间的关系以及行列式值为+1或-1，我们可以通过这种方式大大简化了许多数学问题的计算过程。

四、应用场景

正交阵在许多领域都有广泛的应用。例如在量子力学中，它常常用于描述物理系统的状态变化；在计算机视觉中，正交变换可以用于图像旋转、扭曲和比例调整等；在线性代数中，通过计算一些特定情况下的矩阵分解和最小二乘问题，可以产生许多用于数据处理和分析的有效方法。

总之，正交阵是一种非常重要的数学概念，它在许多领域都有广泛的应用。通过了解其定义、性质和运算规则，我们可以更好地理解其在各种问题中的应用和价值。