exp函数

一、文章标题

exp函数详解

二、文章内容

在数学与计算机科学中，exp函数是应用广泛的一种函数。它是自然数e（约等于2.71828）的指数函数，被广泛应用于概率论、微分方程和复数分析等领域。

一、exp函数的定义

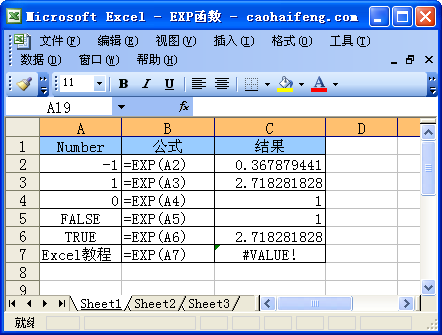
exp函数定义为e的x次方，即exp(x) = e^x。其中，e是自然对数的底数，约等于2.71828。在数学上，我们通常使用e作为底数来构建指数函数，因为它的性质在数学分析中特别重要。

二、exp函数的性质

1. 单调性：exp函数在其定义域内是单调递增的。也就是说，如果x1 < x2，那么exp(x1) < exp(x2)。
2. 指数法则：exp函数满足指数法则，如exp(x+y) = exp(x) * exp(y)。
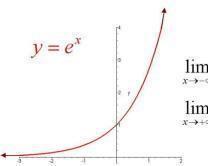
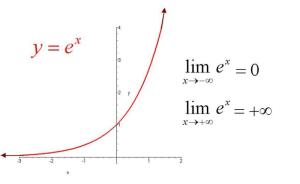
3. 极限性质：当x趋近于无穷大时，exp(x)也趋近于无穷大；当x趋近于负无穷大时，exp(x)趋近于0。

三、exp函数的应用

1. 概率论：在概率论中，exp函数常常用于计算泊松分布和指数分布等概率分布的概率密度函数和累积分布函数。
2. 微分方程：在微分方程中，exp函数是常见的解的形式，如常微分方程中的指数型解。
3. 复数分析：在复数分析中，exp函数被用来描述复数的指数函数，是复平面上的重要映射。

四、Markdown格式下的exp函数公式表示

在Markdown中，我们可以使用e^x或者\exp(x)来表示exp函数。例如：e^x 代表 exp(x)。这样可以让公式更加清晰地展示在文章中。

以上就是关于exp函数的详细介绍。它是一个非常重要的数学函数，在各个领域都有广泛的应用。希望这篇文章能帮助你更好地理解exp函数。