拟合曲线

一、文章标题

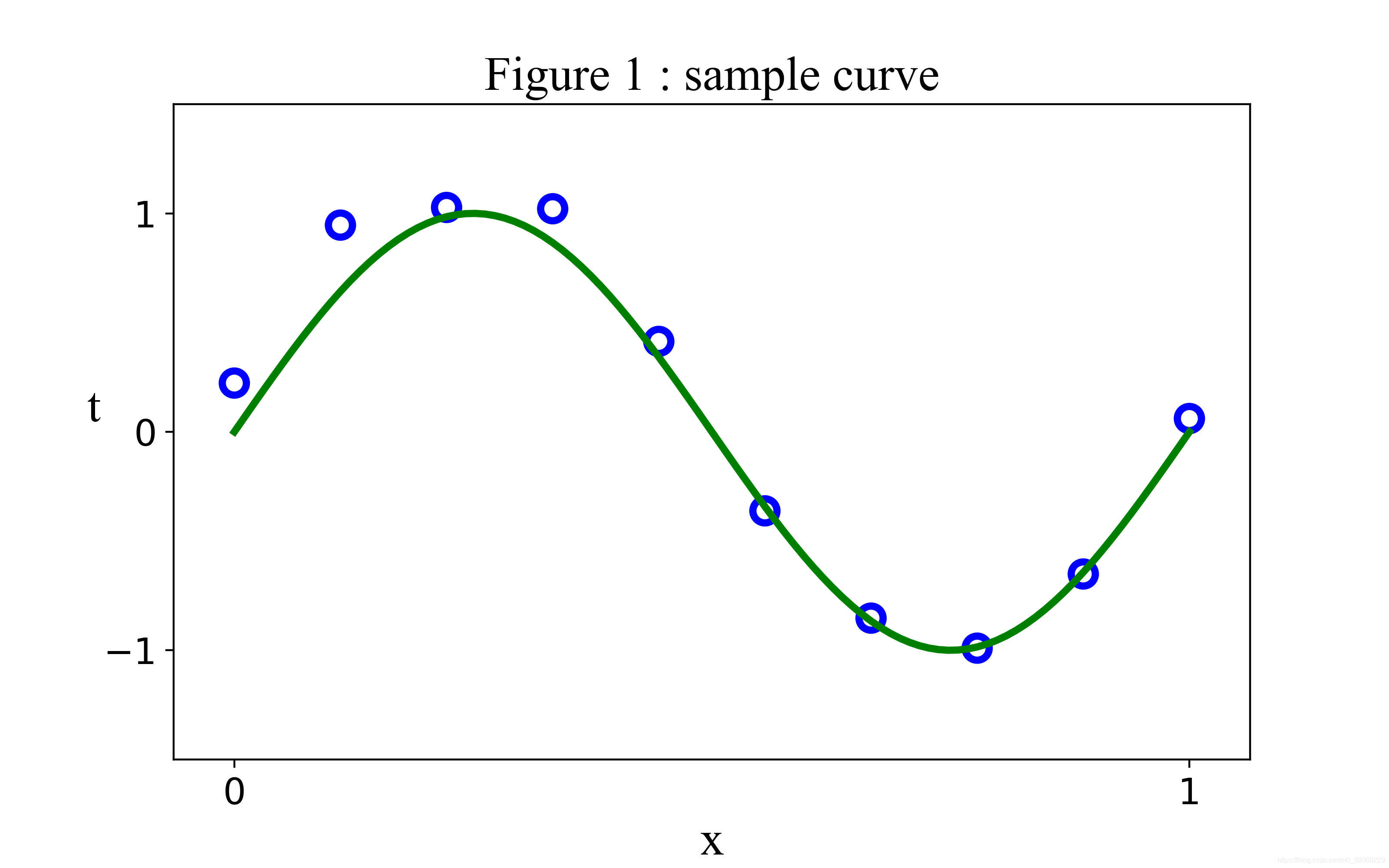
拟合曲线：理解、应用与实例分析

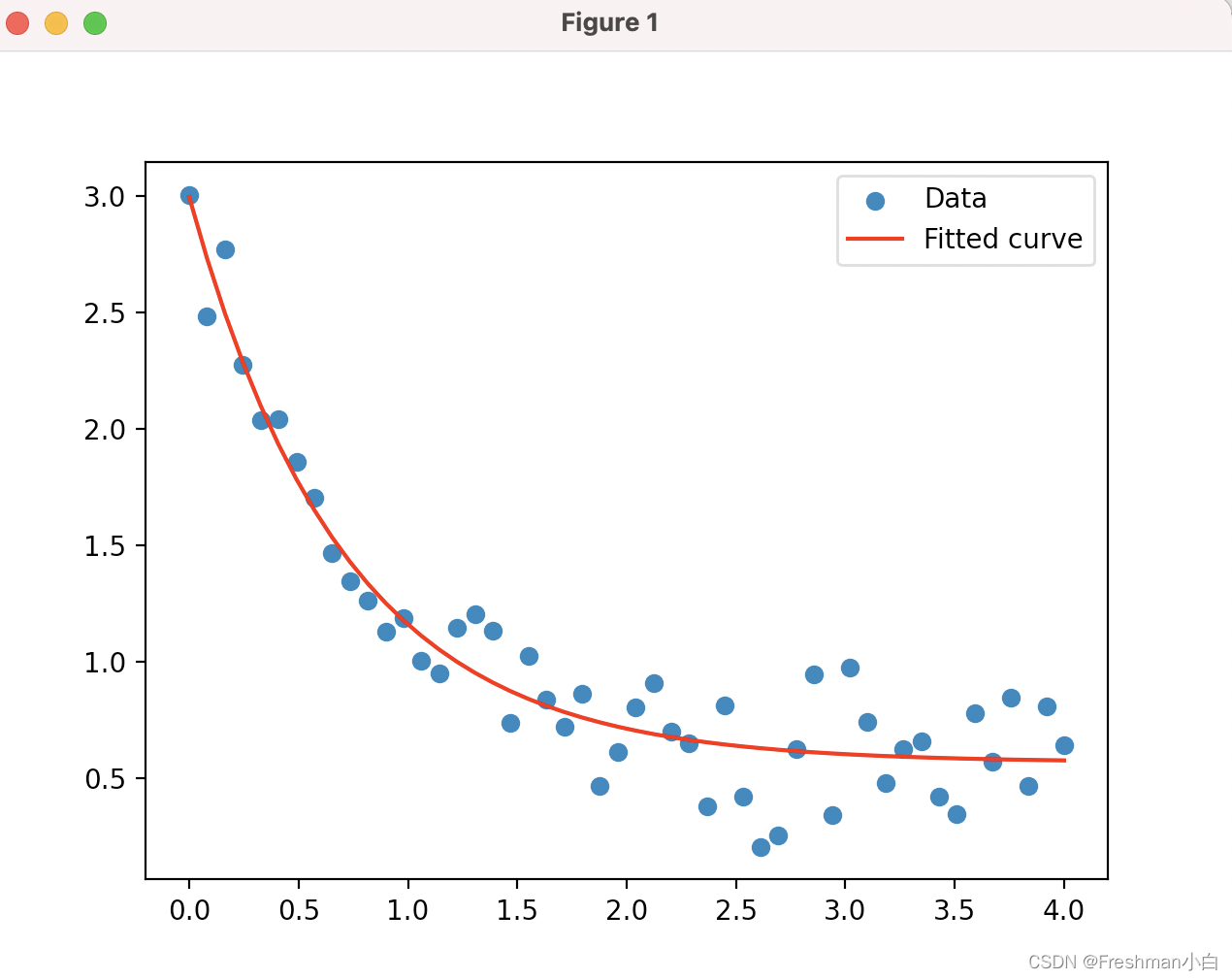
二、文章内容

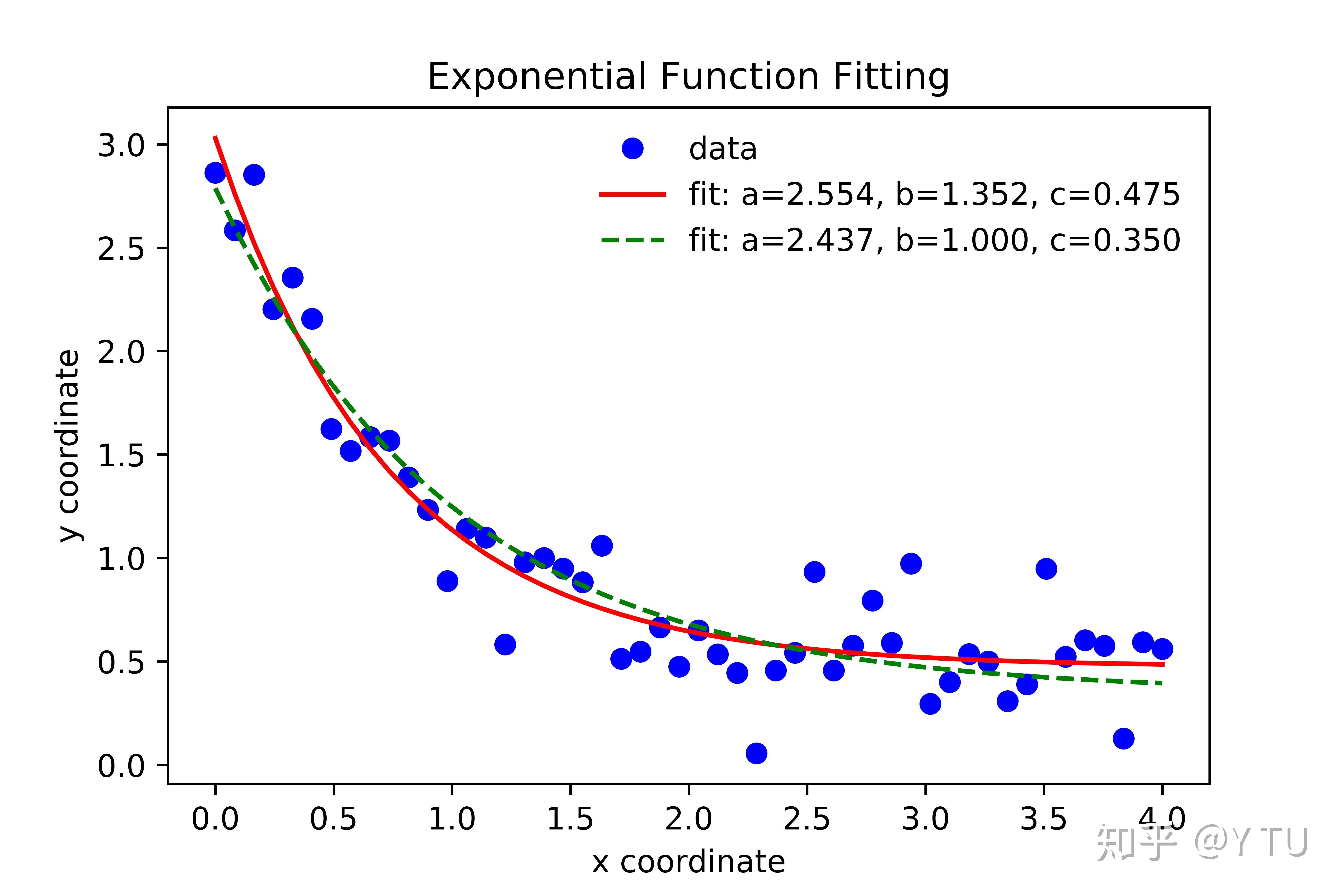
在现代数据处理和数据分析领域，拟合曲线是一种重要的工具，用于根据已有的数据点估计出一种数学模型。这可以帮助我们更好地理解数据的内在规律，并且可以对未知的数据进行预测。在本文中，我们将详细讨论拟合曲线的理解、应用和实例分析。

1. 拟合曲线的理解

拟合曲线是数学模型的一部分，它的目的是用最合适的函数去近似一个给定的数据集。通常，我们使用一些已知的数学函数形式（如线性函数、多项式函数、指数函数等）来描述数据之间的关系。通过最小化误差的平方和或其他优化准则，我们可以得到最佳的拟合参数，使得拟合曲线能够最好地反映数据的特征。

2. 拟合曲线的应用

拟合曲线在许多领域都有广泛的应用。例如，在经济学中，我们可以使用拟合曲线来描述经济增长的规律；在物理学中，拟合曲线可以用于描述物理现象的规律；在医学研究中，拟合曲线可以用于描述药物浓度与时间的关系等。此外，在数据处理和数据分析中，拟合曲线也是一种重要的工具，可以帮助我们更好地理解数据的内在规律，并进行数据预测。

3. 实例分析

以一组气温数据为例，我们可以使用拟合曲线来描述气温随时间的变化规律。假设我们有一组每天的气温数据，我们可以选择一个合适的数学函数形式（如正弦函数或多项式函数）来进行拟合。通过最小化误差的平方和或其他优化准则，我们可以得到最佳的拟合参数。这样，我们就可以用得到的拟合曲线来描述气温随时间的变化规律，并且可以对未来的气温进行预测。

除了气温数据外，拟合曲线还可以应用于许多其他领域的数据分析中。例如，在金融领域中，我们可以使用拟合曲线来描述股票价格的变化规律；在生物医学领域中，我们可以使用拟合曲线来描述生物实验数据的变化趋势等。

总之，拟合曲线是一种重要的数学工具，它可以帮助我们更好地理解数据的内在规律，并进行数据预测。在实际应用中，我们需要根据具体的数据特点选择合适的数学函数形式和优化准则来进行拟合。同时，我们还需要注意拟合曲线的可靠性和有效性问题，避免过度拟合或欠拟合的情况发生。